wishIwasSalludon
broken but not destroyed
- Joined
- Nov 9, 2023
- Posts
- 19,410
- Reputation
- 27,667
In physics, Lagrangian mechanics is a formulation of classical mechanics founded on the stationary-action principle (also known as the principle of least action). It was introduced by the Italian-French mathematician and astronomer Joseph-Louis Lagrange in his presentation to the Turin Academy of Science in 1760[1] culminating in his 1788 grand opus, Mécanique analytique.[2]
Joseph-Louis Lagrange (1736–1813)
Lagrangian mechanics describes a mechanical system as a pair (M, L) consisting of a configuration space M and a smooth function
within that space called a Lagrangian. For many systems, L = T − V, where T and V are the kinetic and potential energy of the system, respectively.[3]
The stationary action principle requires that the action functional of the system derived from L must remain at a stationary point (a maximum, minimum, or saddle) throughout the time evolution of the system. This constraint allows the calculation of the equations of motion of the system using Lagrange's equations.[4]
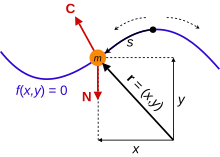Bead constrained to move on a frictionless wire. The wire exerts a reaction force C on the bead to keep it on the wire. The non-constraint force N in this case is gravity. Notice the initial position of the bead on the wire can lead to different motions.
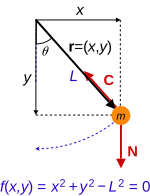Simple pendulum. Since the rod is rigid, the position of the bob is constrained according to the equation f(x, y) = 0, the constraint force C is the tension in the rod. Again the non-constraint force N in this case is gravity.
Newton's laws and the concept of forces are the usual starting point for teaching about mechanical systems.[5] This method works well for many problems, but for others the approach is nightmarishly complicated.[6] For example, in calculation of the motion of a torus rolling on a horizontal surface with a pearl sliding inside, the time-varying constraint forces like the angular velocity of the torus, motion of the pearl in relation to the torus made it difficult to determine the motion of the torus with Newton's equations.[7] Lagrangian mechanics adopts energy rather than force as its basic ingredient,[5] leading to more abstract equations capable of tackling more complex problems.[6]
Particularly, Lagrange's approach was to set up independent generalized coordinates for the position and speed of every object, which allows the writing down of a general form of lagrangian (total kinetic energy minus potential energy of the system) and summing this over all possible paths of motion of the particles yielded a formula for the 'action', which he minimized to give a generalized set of equations. This summed quantity is minimized along the path that the particle actually takes. This choice eliminates the need for the constraint force to enter into the resultant generalized system of equations. There are fewer equations since one is not directly calculating the influence of the constraint on the particle at a given moment.[7]
For a wide variety of physical systems, if the size and shape of a massive object are negligible, it is a useful simplification to treat it as a point particle. For a system of N point particles with masses m1, m2, ..., mN, each particle has a position vector, denoted r1, r2, ..., rN. Cartesian coordinates are often sufficient, so r1 = (x1, y1, z1), r2 = (x2, y2, z2) and so on. In three-dimensional space, each position vector requires three coordinates to uniquely define the location of a point, so there are 3N coordinates to uniquely define the configuration of the system. These are all specific points in space to locate the particles; a general point in space is written r = (x, y, z). The velocity of each particle is how fast the particle moves along its path of motion, and is the time derivative of its position, thus
In Newtonian mechanics, the equations of motionare given by Newton's laws. The second law "net force equals mass times acceleration",
applies to each particle. For an N-particle system in 3 dimensions, there are 3N second-order ordinary differential equations in the positions of the particles to solve for.
Instead of forces, Lagrangian mechanics uses the energies in the system. The central quantity of Lagrangian mechanics is the Lagrangian, a function which summarizes the dynamics of the entire system. Overall, the Lagrangian has units of energy, but no single expression for all physical systems. Any function which generates the correct equations of motion, in agreement with physical laws, can be taken as a Lagrangian. It is nevertheless possible to construct general expressions for large classes of applications. The non-relativistic Lagrangian for a system of particles in the absence of an electromagnetic field is given by[8]
where
is the total kinetic energy of the system, equaling the sum Σ of the kinetic energies of the
particles. Each particle labeled
has mass
and vk2 = vk · vk is the magnitude squared of its velocity, equivalent to the dot product of the velocity with itself.[9]
Kinetic energy T is the energy of the system's motion and is a function only of the velocities vk, not the positions rk, nor time t, so T = T(v1, v2, ...).
V, the potential energy of the system, reflects the energy of interaction between the particles, i.e. how much energy any one particle has due to all the others, together with any external influences. For conservative forces (e.g. Newtonian gravity), it is a function of the position vectors of the particles only, so V = V(r1, r2, ...). For those non-conservative forces which can be derived from an appropriate potential (e.g. electromagnetic potential), the velocities will appear also, V = V(r1, r2, ..., v1, v2, ...).If there is some external field or external driving force changing with time, the potential changes with time, so most generally V = V(r1, r2, ..., v1, v2, ..., t).
As already noted, this form of L is applicable to many important classes of system, but not everywhere. For relativistic Lagrangian mechanics it must be replaced as a whole by a function consistent with special relativity (scalar under Lorentz transformations) or general relativity (4-scalar).[10] Where a magnetic field is present, the expression for the potential energy needs restating.[citation needed] And for dissipative forces (e.g., friction), another function must be introduced alongside Lagrangian often referred to as a "Rayleigh dissipation function" to account for the loss of energy.[11]
One or more of the particles may each be subject to one or more holonomic constraints; such a constraint is described by an equation of the form f(r, t) = 0. If the number of constraints in the system is C, then each constraint has an equation f1(r, t) = 0,f2(r, t) = 0, ..., fC(r, t) = 0, each of which could apply to any of the particles. If particle k is subject to constraint i, then fi(rk, t) = 0. At any instant of time, the coordinates of a constrained particle are linked together and not independent. The constraint equations determine the allowed paths the particles can move along, but not where they are or how fast they go at every instant of time. Nonholonomic constraints depend on the particle velocities, accelerations, or higher derivatives of position. Lagrangian mechanics can only be applied to systems whose constraints, if any, are all holonomic. Three examples of nonholonomic constraints are:[12]when the constraint equations are non-integrable, when the constraints have inequalities, or when the constraints involve complicated non-conservative forces like friction. Nonholonomic constraints require special treatment, and one may have to revert to Newtonian mechanics or use other methods.[13]
If T or V or both depend explicitly on time due to time-varying constraints or external influences, the Lagrangian L(r1, r2, ... v1, v2, ... t) is explicitly time-dependent. If neither the potential nor the kinetic energy depend on time, then the Lagrangian L(r1, r2, ... v1, v2, ...) is explicitly independent of time. In either case, the Lagrangian always has implicit time dependence through the generalized coordinates.
With these definitions, Lagrange's equations of the first kind are[14]
Lagrange's equations (first kind)
where k = 1, 2, ..., N labels the particles, there is a Lagrange multiplier λi for each constraint equation fi, and
are each shorthands for a vector of partial derivatives ∂/∂ with respect to the indicated variables (not a derivative with respect to the entire vector).[nb 1] Each overdot is a shorthand for a time derivative. This procedure does increase the number of equations to solve compared to Newton's laws, from 3N to 3N + C, because there are 3N coupled second-order differential equations in the position coordinates and multipliers, plus Cconstraint equations. However, when solved alongside the position coordinates of the particles, the multipliers can yield information about the constraint forces. The coordinates do not need to be eliminated by solving the constraint equations.
In the Lagrangian, the position coordinates and velocity components are all independent variables, and derivatives of the Lagrangian are taken with respect to these separately according to the usual differentiation rules (e.g. the partial derivative of Lwith respect to the z velocity component of particle 2, defined by vz,2 = dz2/dt, is just ∂L/∂vz,2; no awkward chain rules or total derivatives need to be used to relate the velocity component to the corresponding coordinate z2).
In each constraint equation, one coordinate is redundant because it is determined from the other coordinates. The number of independentcoordinates is therefore n = 3N − C. We can transform each position vector to a common set of ngeneralized coordinates, conveniently written as an n-tuple q = (q1, q2, ... qn), by expressing each position vector, and hence the position coordinates, as functions of the generalized coordinates and time:
The vector q is a point in the configuration space of the system. The time derivatives of the generalized coordinates are called the generalized velocities, and for each particle the transformation of its velocity vector, the total derivative of its position with respect to time, is
Given this vk, the kinetic energy in generalized coordinates depends on the generalized velocities, generalized coordinates, and time if the position vectors depend explicitly on time due to time-varying constraints, so
With these definitions, the Euler–Lagrange equations, or Lagrange's equations of the second kind[15][16][17]
Lagrange's equations (second kind)
are mathematical results from the calculus of variations, which can also be used in mechanics. Substituting in the Lagrangian L(q, dq/dt, t) gives the equations of motion of the system. The number of equations has decreased compared to Newtonian mechanics, from 3N to n = 3N − C coupled second-order differential equations in the generalized coordinates. These equations do not include constraint forces at all, only non-constraint forces need to be accounted for.
Although the equations of motion include partial derivatives, the results of the partial derivatives are still ordinary differential equations in the position coordinates of the particles. The total time derivative denoted d/dt often involves implicit differentiation. Both equations are linear in the Lagrangian, but generally are nonlinear coupled equations in the coordinates.
@cromagnon @ey88 @Debetro @Gengar
Joseph-Louis Lagrange (1736–1813)Lagrangian mechanics describes a mechanical system as a pair (M, L) consisting of a configuration space M and a smooth function
The stationary action principle requires that the action functional of the system derived from L must remain at a stationary point (a maximum, minimum, or saddle) throughout the time evolution of the system. This constraint allows the calculation of the equations of motion of the system using Lagrange's equations.[4]
Introduction
edit
Bead constrained to move on a frictionless wire. The wire exerts a reaction force C on the bead to keep it on the wire. The non-constraint force N in this case is gravity. Notice the initial position of the bead on the wire can lead to different motions.
Simple pendulum. Since the rod is rigid, the position of the bob is constrained according to the equation f(x, y) = 0, the constraint force C is the tension in the rod. Again the non-constraint force N in this case is gravity.Newton's laws and the concept of forces are the usual starting point for teaching about mechanical systems.[5] This method works well for many problems, but for others the approach is nightmarishly complicated.[6] For example, in calculation of the motion of a torus rolling on a horizontal surface with a pearl sliding inside, the time-varying constraint forces like the angular velocity of the torus, motion of the pearl in relation to the torus made it difficult to determine the motion of the torus with Newton's equations.[7] Lagrangian mechanics adopts energy rather than force as its basic ingredient,[5] leading to more abstract equations capable of tackling more complex problems.[6]
Particularly, Lagrange's approach was to set up independent generalized coordinates for the position and speed of every object, which allows the writing down of a general form of lagrangian (total kinetic energy minus potential energy of the system) and summing this over all possible paths of motion of the particles yielded a formula for the 'action', which he minimized to give a generalized set of equations. This summed quantity is minimized along the path that the particle actually takes. This choice eliminates the need for the constraint force to enter into the resultant generalized system of equations. There are fewer equations since one is not directly calculating the influence of the constraint on the particle at a given moment.[7]
For a wide variety of physical systems, if the size and shape of a massive object are negligible, it is a useful simplification to treat it as a point particle. For a system of N point particles with masses m1, m2, ..., mN, each particle has a position vector, denoted r1, r2, ..., rN. Cartesian coordinates are often sufficient, so r1 = (x1, y1, z1), r2 = (x2, y2, z2) and so on. In three-dimensional space, each position vector requires three coordinates to uniquely define the location of a point, so there are 3N coordinates to uniquely define the configuration of the system. These are all specific points in space to locate the particles; a general point in space is written r = (x, y, z). The velocity of each particle is how fast the particle moves along its path of motion, and is the time derivative of its position, thus
Lagrangian
editInstead of forces, Lagrangian mechanics uses the energies in the system. The central quantity of Lagrangian mechanics is the Lagrangian, a function which summarizes the dynamics of the entire system. Overall, the Lagrangian has units of energy, but no single expression for all physical systems. Any function which generates the correct equations of motion, in agreement with physical laws, can be taken as a Lagrangian. It is nevertheless possible to construct general expressions for large classes of applications. The non-relativistic Lagrangian for a system of particles in the absence of an electromagnetic field is given by[8]
Kinetic energy T is the energy of the system's motion and is a function only of the velocities vk, not the positions rk, nor time t, so T = T(v1, v2, ...).
V, the potential energy of the system, reflects the energy of interaction between the particles, i.e. how much energy any one particle has due to all the others, together with any external influences. For conservative forces (e.g. Newtonian gravity), it is a function of the position vectors of the particles only, so V = V(r1, r2, ...). For those non-conservative forces which can be derived from an appropriate potential (e.g. electromagnetic potential), the velocities will appear also, V = V(r1, r2, ..., v1, v2, ...).If there is some external field or external driving force changing with time, the potential changes with time, so most generally V = V(r1, r2, ..., v1, v2, ..., t).
As already noted, this form of L is applicable to many important classes of system, but not everywhere. For relativistic Lagrangian mechanics it must be replaced as a whole by a function consistent with special relativity (scalar under Lorentz transformations) or general relativity (4-scalar).[10] Where a magnetic field is present, the expression for the potential energy needs restating.[citation needed] And for dissipative forces (e.g., friction), another function must be introduced alongside Lagrangian often referred to as a "Rayleigh dissipation function" to account for the loss of energy.[11]
One or more of the particles may each be subject to one or more holonomic constraints; such a constraint is described by an equation of the form f(r, t) = 0. If the number of constraints in the system is C, then each constraint has an equation f1(r, t) = 0,f2(r, t) = 0, ..., fC(r, t) = 0, each of which could apply to any of the particles. If particle k is subject to constraint i, then fi(rk, t) = 0. At any instant of time, the coordinates of a constrained particle are linked together and not independent. The constraint equations determine the allowed paths the particles can move along, but not where they are or how fast they go at every instant of time. Nonholonomic constraints depend on the particle velocities, accelerations, or higher derivatives of position. Lagrangian mechanics can only be applied to systems whose constraints, if any, are all holonomic. Three examples of nonholonomic constraints are:[12]when the constraint equations are non-integrable, when the constraints have inequalities, or when the constraints involve complicated non-conservative forces like friction. Nonholonomic constraints require special treatment, and one may have to revert to Newtonian mechanics or use other methods.[13]
If T or V or both depend explicitly on time due to time-varying constraints or external influences, the Lagrangian L(r1, r2, ... v1, v2, ... t) is explicitly time-dependent. If neither the potential nor the kinetic energy depend on time, then the Lagrangian L(r1, r2, ... v1, v2, ...) is explicitly independent of time. In either case, the Lagrangian always has implicit time dependence through the generalized coordinates.
With these definitions, Lagrange's equations of the first kind are[14]
Lagrange's equations (first kind)
where k = 1, 2, ..., N labels the particles, there is a Lagrange multiplier λi for each constraint equation fi, and
In the Lagrangian, the position coordinates and velocity components are all independent variables, and derivatives of the Lagrangian are taken with respect to these separately according to the usual differentiation rules (e.g. the partial derivative of Lwith respect to the z velocity component of particle 2, defined by vz,2 = dz2/dt, is just ∂L/∂vz,2; no awkward chain rules or total derivatives need to be used to relate the velocity component to the corresponding coordinate z2).
In each constraint equation, one coordinate is redundant because it is determined from the other coordinates. The number of independentcoordinates is therefore n = 3N − C. We can transform each position vector to a common set of ngeneralized coordinates, conveniently written as an n-tuple q = (q1, q2, ... qn), by expressing each position vector, and hence the position coordinates, as functions of the generalized coordinates and time:
The vector q is a point in the configuration space of the system. The time derivatives of the generalized coordinates are called the generalized velocities, and for each particle the transformation of its velocity vector, the total derivative of its position with respect to time, is
Given this vk, the kinetic energy in generalized coordinates depends on the generalized velocities, generalized coordinates, and time if the position vectors depend explicitly on time due to time-varying constraints, so
With these definitions, the Euler–Lagrange equations, or Lagrange's equations of the second kind[15][16][17]
Lagrange's equations (second kind)
are mathematical results from the calculus of variations, which can also be used in mechanics. Substituting in the Lagrangian L(q, dq/dt, t) gives the equations of motion of the system. The number of equations has decreased compared to Newtonian mechanics, from 3N to n = 3N − C coupled second-order differential equations in the generalized coordinates. These equations do not include constraint forces at all, only non-constraint forces need to be accounted for.
Although the equations of motion include partial derivatives, the results of the partial derivatives are still ordinary differential equations in the position coordinates of the particles. The total time derivative denoted d/dt often involves implicit differentiation. Both equations are linear in the Lagrangian, but generally are nonlinear coupled equations in the coordinates.
@cromagnon @ey88 @Debetro @Gengar
