D
Deleted member 13787
Fire
- Joined
- May 3, 2021
- Posts
- 26,417
- Reputation
- 71,582
Quantum entanglement is a physical phenomenon that occurs when a group of particles are generated, interact, or share spatial proximity in a way such that the quantum state of each particle of the group cannot be described independently of the state of the others, including when the particles are separated by a large distance. The topic of quantum entanglement is at the heart of the disparity between classical and quantum physics: entanglement is a primary feature of quantum mechanics lacking in classical mechanics.
Measurements of physical properties such as position, momentum, spin, and polarization performed on entangled particles can, in some cases, be found to be perfectly correlated. For example, if a pair of entangled particles is generated such that their total spin is known to be zero, and one particle is found to have clockwise spin on a first axis, then the spin of the other particle, measured on the same axis, is found to be counterclockwise. However, this behavior gives rise to seemingly paradoxical effects: any measurement of a particle's properties results in an irreversible wave function collapse of that particle and changes the original quantum state. With entangled particles, such measurements affect the entangled system as a whole.
Such phenomena were the subject of a 1935 paper by Albert Einstein, Boris Podolsky, and Nathan Rosen,[1] and several papers by Erwin Schrödinger shortly thereafter,[2][3] describing what came to be known as the EPR paradox. Einstein and others considered such behavior impossible, as it violated the local realism view of causality (Einstein referring to it as "spooky action at a distance")[4] and argued that the accepted formulation of quantum mechanics must therefore be incomplete.
Later, however, the counterintuitive predictions of quantum mechanics were verified[5][6][7] in tests where polarization or spin of entangled particles was measured at separate locations, statistically violating Bell's inequality. In earlier tests, it couldn't be ruled out that the result at one point could have been subtly transmitted to the remote point, affecting the outcome at the second location.[7] However, so-called "loophole-free" Bell tests have been performed where the locations were sufficiently separated that communications at the speed of light would have taken longer—in one case, 10,000 times longer—than the interval between the measurements.[6][5]
According to some interpretations of quantum mechanics, the effect of one measurement occurs instantly. Other interpretations which don't recognize wavefunction collapse dispute that there is any "effect" at all. However, all interpretations agree that entanglement produces correlation between the measurements and that the mutual information between the entangled particles can be exploited, but that any transmission of information at faster-than-light speeds is impossible.[8][9]
Quantum entanglement has been demonstrated experimentally with photons,[10][11] neutrinos,[12] electrons,[13][14] molecules as large as buckyballs,[15][16] and even small diamonds.[17][18] The utilization of entanglement in communication, computation and quantum radar is a very active area of research and development.

Spontaneous parametric down-conversion process can split photons into type II photon pairs with mutually perpendicular polarization.
Schrödinger shortly thereafter published a seminal paper defining and discussing the notion of "entanglement." In the paper, he recognized the importance of the concept, and stated:[2] "I would not call [entanglement] one but rather the characteristic trait of quantum mechanics, the one that enforces its entire departure from classical lines of thought." Like Einstein, Schrödinger was dissatisfied with the concept of entanglement, because it seemed to violate the speed limit on the transmission of information implicit in the theory of relativity.[20] Einstein later famously derided entanglement as "spukhafte Fernwirkung"[21] or "spooky action at a distance."
The EPR paper generated significant interest among physicists, which inspired much discussion about the foundations of quantum mechanics (perhaps most famously Bohm's interpretation of quantum mechanics), but produced relatively little other published work. Despite the interest, the weak point in EPR's argument was not discovered until 1964, when John Stewart Bell proved that one of their key assumptions, the principle of locality, as applied to the kind of hidden variables interpretation hoped for by EPR, was mathematically inconsistent with the predictions of quantum theory.
Specifically, Bell demonstrated an upper limit, seen in Bell's inequality, regarding the strength of correlations that can be produced in any theory obeying local realism, and showed that quantum theory predicts violations of this limit for certain entangled systems.[22] His inequality is experimentally testable, and there have been numerous relevant experiments, starting with the pioneering work of Stuart Freedman and John Clauser in 1972[23] and Alain Aspect's experiments in 1982.[24] An early experimental breakthrough was due to Carl Kocher,[10][11] who already in 1967 presented an apparatus in which two photons successively emitted from a calcium atom were shown to be entangled – the first case of entangled visible light. The two photons passed diametrically positioned parallel polarizers with higher probability than classically predicted but with correlations in quantitative agreement with quantum mechanical calculations. He also showed that the correlation varied only upon (as cosine square of) the angle between the polarizer settings[11] and decreased exponentially with time lag between emitted photons.[25] Kocher’s apparatus, equipped with better polarizers, was used by Freedman and Clauser who could confirm the cosine square dependence and use it to demonstrate a violation of Bell’s inequality for a set of fixed angles.[23] All these experiments have shown agreement with quantum mechanics rather than the principle of local realism.
For decades, each had left open at least one loophole by which it was possible to question the validity of the results. However, in 2015 an experiment was performed that simultaneously closed both the detection and locality loopholes, and was heralded as "loophole-free"; this experiment ruled out a large class of local realism theories with certainty.[26] Alain Aspect notes that the "setting-independence loophole" – which he refers to as "far-fetched", yet, a "residual loophole" that "cannot be ignored" – has yet to be closed, and the free-will / superdeterminism loophole is unclosable; saying "no experiment, as ideal as it is, can be said to be totally loophole-free."[27]
Bell's work raised the possibility of using these super-strong correlations as a resource for communication. It led to the 1984 discovery of quantum key distribution protocols, most famously BB84 by Charles H. Bennett and Gilles Brassard[28] and E91 by Artur Ekert.[29] Although BB84 does not use entanglement, Ekert's protocol uses the violation of a Bell's inequality as a proof of security.

Article headline regarding the Einstein–Podolsky–Rosen paradox (EPR paradox) paper, in the May 4, 1935 issue of The New York Times.
Quantum systems can become entangled through various types of interactions. For some ways in which entanglement may be achieved for experimental purposes, see the section below on methods. Entanglement is broken when the entangled particles decohere through interaction with the environment; for example, when a measurement is made.[30]
As an example of entanglement: a subatomic particle decays into an entangled pair of other particles. The decay events obey the various conservation laws, and as a result, the measurement outcomes of one daughter particle must be highly correlated with the measurement outcomes of the other daughter particle (so that the total momenta, angular momenta, energy, and so forth remains roughly the same before and after this process). For instance, a spin-zero particle could decay into a pair of spin-½ particles. Since the total spin before and after this decay must be zero (conservation of angular momentum), whenever the first particle is measured to be spin up on some axis, the other, when measured on the same axis, is always found to be spin down. (This is called the spin anti-correlated case; and if the prior probabilities for measuring each spin are equal, the pair is said to be in the singlet state.)
The above result may or may not be perceived as surprising. A classical system would display the same property, and a hidden variable theory (see below) would certainly be required to do so, based on conservation of angular momentum in classical and quantum mechanics alike. The difference is that a classical system has definite values for all the observables all along, while the quantum system does not. In a sense to be discussed below, the quantum system considered here seems to acquire a probability distribution for the outcome of a measurement of the spin along any axis of the other particle upon measurement of the first particle. This probability distribution is in general different from what it would be without measurement of the first particle. This may certainly be perceived as surprising in the case of spatially separated entangled particles.
The distance and timing of the measurements can be chosen so as to make the interval between the two measurements spacelike, hence, any causal effect connecting the events would have to travel faster than light. According to the principles of special relativity, it is not possible for any information to travel between two such measuring events. It is not even possible to say which of the measurements came first. For two spacelike separated events x1 and x2 there are inertial frames in which x1 is first and others in which x2 is first. Therefore, the correlation between the two measurements cannot be explained as one measurement determining the other: different observers would disagree about the role of cause and effect.
(In fact similar paradoxes can arise even without entanglement: the position of a single particle is spread out over space, and two widely separated detectors attempting to detect the particle in two different places must instantaneously attain appropriate correlation, so that they do not both detect the particle.)
The fundamental issue about measuring spin along different axes is that these measurements cannot have definite values at the same time―they are incompatible in the sense that these measurements' maximum simultaneous precision is constrained by the uncertainty principle. This is contrary to what is found in classical physics, where any number of properties can be measured simultaneously with arbitrary accuracy. It has been proven mathematically that compatible measurements cannot show Bell-inequality-violating correlations,[37] and thus entanglement is a fundamentally non-classical phenomenon.
In three independent experiments in 2013 it was shown that classically communicated separable quantum states can be used to carry entangled states.[41] The first loophole-free Bell test was held in TU Delft in 2015 confirming the violation of Bell inequality.[42]
In August 2014, Brazilian researcher Gabriela Barreto Lemos and team were able to "take pictures" of objects using photons that had not interacted with the subjects, but were entangled with photons that did interact with such objects. Lemos, from the University of Vienna, is confident that this new quantum imaging technique could find application where low light imaging is imperative, in fields like biological or medical imaging.[43]
From 2016 various companies like IBM, Microsoft etc. have successfully created quantum computers and allowed developers and tech enthusiasts to openly experiment with concepts of quantum mechanics including quantum entanglement.[44]
In short, entanglement of a state shared by two parties is necessary but not sufficient for that state to be non-local. It is important to recognize that entanglement is more commonly viewed as an algebraic concept, noted for being a prerequisite to non-locality as well as to quantum teleportation and to superdense coding, whereas non-locality is defined according to experimental statistics and is much more involved with the foundations and interpretations of quantum mechanics.[56]
{\displaystyle H_{A}\otimes H_{B}.}

If the first system is in state {\displaystyle \scriptstyle |\psi \rangle _{A}} and the second in state {\displaystyle \scriptstyle |\phi \rangle _{B}}, the state of the composite system is
{\displaystyle |\psi \rangle _{A}\otimes |\phi \rangle _{B}.}
States of the composite system that can be represented in this form are called separable states, or product states.
Not all states are separable states (and thus product states). Fix a basis {\displaystyle \scriptstyle \{|i\rangle _{A}\}} for HA and a basis {\displaystyle \scriptstyle \{|j\rangle _{B}\}} for HB. The most general state in HA ⊗ HB is of the form
{\displaystyle |\psi \rangle _{AB}=\sum _{i,j}c_{ij}|i\rangle _{A}\otimes |j\rangle _{B}}
 .
.
This state is separable if there exist vectors {\displaystyle \scriptstyle [c_{i}^{A}],[c_{j}^{B}]} so that {\displaystyle \scriptstyle c_{ij}=c_{i}^{A}c_{j}^{B},}
 yielding {\displaystyle \scriptstyle |\psi \rangle _{A}=\sum _{i}c_{i}^{A}|i\rangle _{A}}
yielding {\displaystyle \scriptstyle |\psi \rangle _{A}=\sum _{i}c_{i}^{A}|i\rangle _{A}}
 and {\displaystyle \scriptstyle |\phi \rangle _{B}=\sum _{j}c_{j}^{B}|j\rangle _{B}.}
and {\displaystyle \scriptstyle |\phi \rangle _{B}=\sum _{j}c_{j}^{B}|j\rangle _{B}.}
 It is inseparable if for any vectors {\displaystyle \scriptstyle [c_{i}^{A}],[c_{j}^{B}]}
It is inseparable if for any vectors {\displaystyle \scriptstyle [c_{i}^{A}],[c_{j}^{B}]}
![\scriptstyle [c^A_i],[c^B_j] \scriptstyle [c^A_i],[c^B_j]](/proxy.php?image=https%3A%2F%2Fwikimedia.org%2Fapi%2Frest_v1%2Fmedia%2Fmath%2Frender%2Fsvg%2Fe589a6b1f44cb3d763716fd930b19f7184291fd0&hash=ac208b8b6db5f148bb4a3995a7f7e1fd) at least for one pair of coordinates {\displaystyle \scriptstyle c_{i}^{A},c_{j}^{B}} we have {\displaystyle \scriptstyle c_{ij}\neq c_{i}^{A}c_{j}^{B}.} If a state is inseparable, it is called an 'entangled state'.
at least for one pair of coordinates {\displaystyle \scriptstyle c_{i}^{A},c_{j}^{B}} we have {\displaystyle \scriptstyle c_{ij}\neq c_{i}^{A}c_{j}^{B}.} If a state is inseparable, it is called an 'entangled state'.
For example, given two basis vectors {\displaystyle \scriptstyle \{|0\rangle _{A},|1\rangle _{A}\}} of HA and two basis vectors {\displaystyle \scriptstyle \{|0\rangle _{B},|1\rangle _{B}\}} of HB, the following is an entangled state:
{\displaystyle {\tfrac {1}{\sqrt {2}}}\left(|0\rangle _{A}\otimes |1\rangle _{B}-|1\rangle _{A}\otimes |0\rangle _{B}\right).}

If the composite system is in this state, it is impossible to attribute to either system A or system B a definite pure state. Another way to say this is that while the von Neumann entropy of the whole state is zero (as it is for any pure state), the entropy of the subsystems is greater than zero. In this sense, the systems are "entangled". This has specific empirical ramifications for interferometry.[57] The above example is one of four Bell states, which are (maximally) entangled pure states (pure states of the HA ⊗ HB space, but which cannot be separated into pure states of each HA and HB).
Now suppose Alice is an observer for system A, and Bob is an observer for system B. If in the entangled state given above Alice makes a measurement in the {\displaystyle \scriptstyle \{|0\rangle ,|1\rangle \}} eigenbasis of A, there are two possible outcomes, occurring with equal probability:[58]
The outcome of Alice's measurement is random. Alice cannot decide which state to collapse the composite system into, and therefore cannot transmit information to Bob by acting on her system. Causality is thus preserved, in this particular scheme. For the general argument, see no-communication theorem.
{\displaystyle \rho =\sum _{i}w_{i}|\alpha _{i}\rangle \langle \alpha _{i}|,}

where the wi are positive-valued probabilities (they sum up to 1), the vectors αi are unit vectors, and in the infinite-dimensional case, we would take the closure of such states in the trace norm. We can interpret ρ as representing an ensemble where wi is the proportion of the ensemble whose states are {\displaystyle |\alpha _{i}\rangle }. When a mixed state has rank 1, it therefore describes a 'pure ensemble'. When there is less than total information about the state of a quantum system we need density matrices to represent the state.
Experimentally, a mixed ensemble might be realized as follows. Consider a "black box" apparatus that spits electrons towards an observer. The electrons' Hilbert spaces are identical. The apparatus might produce electrons that are all in the same state; in this case, the electrons received by the observer are then a pure ensemble. However, the apparatus could produce electrons in different states. For example, it could produce two populations of electrons: one with state {\displaystyle |\mathbf {z} +\rangle } with spins aligned in the positive z direction, and the other with state {\displaystyle |\mathbf {y} -\rangle }
 with spins aligned in the negative y direction. Generally, this is a mixed ensemble, as there can be any number of populations, each corresponding to a different state.
with spins aligned in the negative y direction. Generally, this is a mixed ensemble, as there can be any number of populations, each corresponding to a different state.
Following the definition above, for a bipartite composite system, mixed states are just density matrices on HA ⊗ HB. That is, it has the general form
{\displaystyle \rho =\sum _{i}w_{i}\left[\sum _{j}{\bar {c}}_{ij}(|\alpha _{ij}\rangle \otimes |\beta _{ij}\rangle )\right]\left[\sum _{k}c_{ik}(\langle \alpha _{ik}|\otimes \langle \beta _{ik}|)\right]}
![{\displaystyle \rho =\sum _{i}w_{i}\left[\sum _{j}{\bar {c}}_{ij}(|\alpha _{ij}\rangle \otimes |\beta _{ij}\rangle )\right]\left[\sum _{k}c_{ik}(\langle \alpha _{ik}|\otimes \langle \beta _{ik}|)\right]} {\displaystyle \rho =\sum _{i}w_{i}\left[\sum _{j}{\bar {c}}_{ij}(|\alpha _{ij}\rangle \otimes |\beta _{ij}\rangle )\right]\left[\sum _{k}c_{ik}(\langle \alpha _{ik}|\otimes \langle \beta _{ik}|)\right]}](/proxy.php?image=https%3A%2F%2Fwikimedia.org%2Fapi%2Frest_v1%2Fmedia%2Fmath%2Frender%2Fsvg%2Fcbf2f7c56adc4e273d3e3c73ee6a66e190c3f35c&hash=9d67baa21ff4b8323dc4b702bbc191f7)
where the wi are positively valued probabilities, {\displaystyle \sum _{j}|c_{ij}|^{2}=1}, and the vectors are unit vectors. This is self-adjoint and positive and has trace 1.
Extending the definition of separability from the pure case, we say that a mixed state is separable if it can be written as[59]: 131–132
{\displaystyle \rho =\sum _{i}w_{i}\rho _{i}^{A}\otimes \rho _{i}^{B},}
where the wi are positively valued probabilities and the {\displaystyle \rho _{i}^{A}}'s and {\displaystyle \rho _{i}^{B}}'s are themselves mixed states (density operators) on the subsystems A and B respectively. In other words, a state is separable if it is a probability distribution over uncorrelated states, or product states. By writing the density matrices as sums of pure ensembles and expanding, we may assume without loss of generality that {\displaystyle \rho _{i}^{A}} and {\displaystyle \rho _{i}^{B}} are themselves pure ensembles. A state is then said to be entangled if it is not separable.
In general, finding out whether or not a mixed state is entangled is considered difficult. The general bipartite case has been shown to be NP-hard.[60] For the 2 × 2 and 2 × 3 cases, a necessary and sufficient criterion for separability is given by the famous Positive Partial Transpose (PPT) condition.[61]
{\displaystyle |\Psi \rangle \in H_{A}\otimes H_{B}.}

As indicated above, in general there is no way to associate a pure state to the component system A. However, it still is possible to associate a density matrix. Let
{\displaystyle \rho _{T}=|\Psi \rangle \;\langle \Psi |}
 .
.
which is the projection operator onto this state. The state of A is the partial trace of ρT over the basis of system B:
{\displaystyle \rho _{A}\ {\stackrel {\mathrm {def} }{=}}\ \sum _{j}^{N_{B}}\left(I_{A}\otimes \langle j|_{B}\right)\left(|\Psi \rangle \langle \Psi |\right)\left(I_{A}\otimes |j\rangle _{B}\right)={\hbox{Tr}}_{B}\;\rho _{T}.}

The sum occurs over {\displaystyle N_{B}:=dim(H_{B})} and {\displaystyle I_{A}} the identity operator in {\displaystyle H_{A}}. ρA is sometimes called the reduced density matrix of ρ on subsystem A. Colloquially, we "trace out" system B to obtain the reduced density matrix on A.
For example, the reduced density matrix of A for the entangled state
{\displaystyle {\tfrac {1}{\sqrt {2}}}\left(|0\rangle _{A}\otimes |1\rangle _{B}-|1\rangle _{A}\otimes |0\rangle _{B}\right),}

discussed above is
{\displaystyle \rho _{A}={\tfrac {1}{2}}\left(|0\rangle _{A}\langle 0|_{A}+|1\rangle _{A}\langle 1|_{A}\right)}
This demonstrates that, as expected, the reduced density matrix for an entangled pure ensemble is a mixed ensemble. Also not surprisingly, the density matrix of A for the pure product state {\displaystyle |\psi \rangle _{A}\otimes |\phi \rangle _{B}} discussed above is
{\displaystyle \rho _{A}=|\psi \rangle _{A}\langle \psi |_{A}}.
In general, a bipartite pure state ρ is entangled if and only if its reduced states are mixed rather than pure.
The reduced density matrix also was evaluated for XY spin chains, where it has full rank. It was proved that in the thermodynamic limit, the spectrum of the reduced density matrix of a large block of spins is an exact geometric sequence[64] in this case.
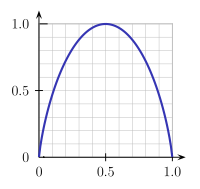
The plot of von Neumann entropy Vs Eigenvalue for a bipartite 2-level pure state. When the eigenvalue has value .5, von Neumann entropy is at a maximum, corresponding to maximum entanglement.
In classical information theory H, the Shannon entropy, is associated to a probability distribution,{\displaystyle p_{1},\cdots ,p_{n}}
 , in the following way:[72]
, in the following way:[72]
{\displaystyle H(p_{1},\cdots ,p_{n})=-\sum _{i}p_{i}\log _{2}p_{i}.}
Since a mixed state ρ is a probability distribution over an ensemble, this leads naturally to the definition of the von Neumann entropy:
{\displaystyle S(\rho )=-{\hbox{Tr}}\left(\rho \log _{2}{\rho }\right).}
In general, one uses the Borel functional calculus to calculate a non-polynomial function such as log2(ρ). If the nonnegative operator ρ acts on a finite-dimensional Hilbert space and has eigenvalues {\displaystyle \lambda _{1},\cdots ,\lambda _{n}}, log2(ρ) turns out to be nothing more than the operator with the same eigenvectors, but the eigenvalues {\displaystyle \log _{2}(\lambda _{1}),\cdots ,\log _{2}(\lambda _{n})}. The Shannon entropy is then:
{\displaystyle S(\rho )=-{\hbox{Tr}}\left(\rho \log _{2}{\rho }\right)=-\sum _{i}\lambda _{i}\log _{2}\lambda _{i}}
 .
.
Since an event of probability 0 should not contribute to the entropy, and given that
{\displaystyle \lim _{p\to 0}p\log p=0,}

the convention 0 log(0) = 0 is adopted. This extends to the infinite-dimensional case as well: if ρ has spectral resolution
{\displaystyle \rho =\int \lambda dP_{\lambda },}
assume the same convention when calculating
{\displaystyle \rho \log _{2}\rho =\int \lambda \log _{2}\lambda dP_{\lambda }.}
As in statistical mechanics, the more uncertainty (number of microstates) the system should possess, the larger the entropy. For example, the entropy of any pure state is zero, which is unsurprising since there is no uncertainty about a system in a pure state. The entropy of any of the two subsystems of the entangled state discussed above is log(2) (which can be shown to be the maximum entropy for 2 × 2 mixed states).
For bipartite pure states, the von Neumann entropy of reduced states is the unique measure of entanglement in the sense that it is the only function on the family of states that satisfies certain axioms required of an entanglement measure[citation needed].
It is a classical result that the Shannon entropy achieves its maximum at, and only at, the uniform probability distribution {1/n,...,1/n}. Therefore, a bipartite pure state ρ ∈ HA ⊗ HB is said to be a maximally entangled state if the reduced state of each subsystem of ρ is the diagonal matrix
{\displaystyle {\begin{bmatrix}{\frac {1}{n}}&&\\&\ddots &\\&&{\frac {1}{n}}\end{bmatrix}}.}
For mixed states, the reduced von Neumann entropy is not the only reasonable entanglement measure.
As an aside, the information-theoretic definition is closely related to entropy in the sense of statistical mechanics[citation needed] (comparing the two definitions in the present context, it is customary to set the Boltzmann constant k = 1). For example, by properties of the Borel functional calculus, we see that for any unitary operator U,
{\displaystyle S(\rho )=S\left(U\rho U^{*}\right).}
Indeed, without this property, the von Neumann entropy would not be well-defined.
In particular, U could be the time evolution operator of the system, i.e.,
{\displaystyle U(t)=\exp \left({\frac {-iHt}{\hbar }}\right),}

where H is the Hamiltonian of the system. Here the entropy is unchanged.
The reversibility of a process is associated with the resulting entropy change, i.e., a process is reversible if, and only if, it leaves the entropy of the system invariant. Therefore, the march of the arrow of time towards thermodynamic equilibrium is simply the growing spread of quantum entanglement.[74] This provides a connection between quantum information theory and thermodynamics.
Rényi entropy also can be used as a measure of entanglement.
Among the best-known applications of entanglement are superdense coding and quantum teleportation.[76]
Most researchers believe that entanglement is necessary to realize quantum computing (although this is disputed by some).[77]
Entanglement is used in some protocols of quantum cryptography.[78][79] This is because the "shared noise" of entanglement makes for an excellent one-time pad. Moreover, since measurement of either member of an entangled pair destroys the entanglement they share, entanglement-based quantum cryptography allows the sender and receiver to more easily detect the presence of an interceptor.[citation needed]
In interferometry, entanglement is necessary for surpassing the standard quantum limit and achieving the Heisenberg limit.[80]
For two qubits, the Bell states are
{\displaystyle |\Phi ^{\pm }\rangle ={\frac {1}{\sqrt {2}}}(|0\rangle _{A}\otimes |0\rangle _{B}\pm |1\rangle _{A}\otimes |1\rangle _{B})}
 {\displaystyle |\Psi ^{\pm }\rangle ={\frac {1}{\sqrt {2}}}(|0\rangle _{A}\otimes |1\rangle _{B}\pm |1\rangle _{A}\otimes |0\rangle _{B})}.
{\displaystyle |\Psi ^{\pm }\rangle ={\frac {1}{\sqrt {2}}}(|0\rangle _{A}\otimes |1\rangle _{B}\pm |1\rangle _{A}\otimes |0\rangle _{B})}.
These four pure states are all maximally entangled (according to the entropy of entanglement) and form an orthonormal basis (linear algebra) of the Hilbert space of the two qubits. They play a fundamental role in Bell's theorem.
For M>2 qubits, the GHZ state is
{\displaystyle |\mathrm {GHZ} \rangle ={\frac {|0\rangle ^{\otimes M}+|1\rangle ^{\otimes M}}{\sqrt {2}}},}
which reduces to the Bell state {\displaystyle |\Phi ^{+}\rangle } for {\displaystyle M=2}. The traditional GHZ state was defined for {\displaystyle M=3}. GHZ states are occasionally extended to qudits, i.e., systems of d rather than 2 dimensions.
Also for M>2 qubits, there are spin squeezed states.[81] Spin squeezed states are a class of squeezed coherent states satisfying certain restrictions on the uncertainty of spin measurements, and are necessarily entangled.[82] Spin squeezed states are good candidates for enhancing precision measurements using quantum entanglement.[83]
For two bosonic modes, a NOON state is
{\displaystyle |\psi _{\text{NOON}}\rangle ={\frac {|N\rangle _{a}|0\rangle _{b}+|{0}\rangle _{a}|{N}\rangle _{b}}{\sqrt {2}}},\,}

This is like the Bell state {\displaystyle |\Psi ^{+}\rangle } except the basis kets 0 and 1 have been replaced with "the N photons are in one mode" and "the N photons are in the other mode".
Finally, there also exist twin Fock states for bosonic modes, which can be created by feeding a Fock state into two arms leading to a beam splitter. They are the sum of multiple of NOON states, and can used to achieve the Heisenberg limit.[84]
For the appropriately chosen measure of entanglement, Bell, GHZ, and NOON states are maximally entangled while spin squeezed and twin Fock states are only partially entangled. The partially entangled states are generally easier to prepare experimentally.
It is also possible to create entanglement between quantum systems that never directly interacted, through the use of entanglement swapping. Two independently prepared, identical particles may also be entangled if their wave functions merely spatially overlap, at least partially.[86]
{\displaystyle \displaystyle {\rho =\sum _{j}p_{j}\rho _{j}^{(A)}\otimes \rho _{j}^{(B)}}}
with {\displaystyle 1\geq p_{j}\geq 0} probabilities. By definition, a state is entangled if it is not separable.
For 2-Qubit and Qubit-Qutrit systems (2 × 2 and 2 × 3 respectively) the simple Peres–Horodecki criterion provides both a necessary and a sufficient criterion for separability, and thus—inadvertently—for detecting entanglement. However, for the general case, the criterion is merely a necessary one for separability, as the problem becomes NP-hard when generalized.[87][88] Other separability criteria include (but not limited to) the range criterion, reduction criterion, and those based on uncertainty relations.[89][90][91][92] See Ref.[93] for a review of separability criteria in discrete-variable systems and Ref.[94] for a review on techniques and challenges in experimental entanglement certification in discrete-variable systems.
A numerical approach to the problem is suggested by Jon Magne Leinaas, Jan Myrheim and Eirik Ovrum in their paper "Geometrical aspects of entanglement".[95] Leinaas et al. offer a numerical approach, iteratively refining an estimated separable state towards the target state to be tested, and checking if the target state can indeed be reached. An implementation of the algorithm (including a built-in Peres-Horodecki criterion testing) is "StateSeparator" web-app.
In continuous variable systems, the Peres-Horodecki criterion also applies. Specifically, Simon[96] formulated a particular version of the Peres-Horodecki criterion in terms of the second-order moments of canonical operators and showed that it is necessary and sufficient for {\displaystyle 1\oplus 1}-mode Gaussian states (see Ref.[97] for a seemingly different but essentially equivalent approach). It was later found[98] that Simon's condition is also necessary and sufficient for {\displaystyle 1\oplus n}-mode Gaussian states, but no longer sufficient for {\displaystyle 2\oplus 2}-mode Gaussian states. Simon's condition can be generalized by taking into account the higher order moments of canonical operators[99][100] or by using entropic measures.[101][102]
In 2016 China launched the world’s first quantum communications satellite.[103] The $100m Quantum Experiments at Space Scale (QUESS) mission was launched on Aug 16, 2016, from the Jiuquan Satellite Launch Center in northern China at 01:40 local time.
For the next two years, the craft – nicknamed "Micius" after the ancient Chinese philosopher – will demonstrate the feasibility of quantum communication between Earth and space, and test quantum entanglement over unprecedented distances.
In the June 16, 2017, issue of Science, Yin et al. report setting a new quantum entanglement distance record of 1,203 km, demonstrating the survival of a two-photon pair and a violation of a Bell inequality, reaching a CHSH valuation of 2.37 ± 0.09, under strict Einstein locality conditions, from the Micius satellite to bases in Lijian, Yunnan and Delingha, Quinhai, increasing the efficiency of transmission over prior fiberoptic experiments by an order of magnitude.[104][105]
It should not be supposed that Einstein’s notion of a complete theory included the requirement that the theory should be deterministic. Rather, he required certain conditions of separability and locality for composite systems consisting of separated component systems: each component system separately should be characterized by its own properties (its own ‘being-thus,’ as Einstein put it — ‘So-sein’ in German), and it should be impossible to alter the properties of a distant system instantaneously (or the probabilities of these properties) by acting on a local system. In later analyses, notably in Bell’s argument for the nonlocality of quantum correlations, it became apparent that these conditions, suitably formulated as probability constraints, are equivalent to the requirement that statistical correlations between separated systems should be reducible to probability distributions over common causes (deterministic or stochastic) in the sense of Reichenbach. (See the entries on Bell’s theorem and Reichenbach’s common cause principle.)
In the original EPR article, two particles are prepared from a source in a certain ‘pure’ quantum state of the composite system (a state that cannot be expressed as a mixture or probability distribution of other pure quantum states, and cannot be reduced to a pure quantum state of each particle separately). After the particles move apart, there are ‘matching’ correlations between both the positions of the two particles and their momenta: a measurement of either position or momentum on a particular particle will allow the prediction, with certainty, of the outcome of a position measurement or momentum measurement, respectively, on the other particle. These measurements are mutually exclusive: either a position measurement can be performed, or a momentum measurement, but not both simultaneously. The subsequent measurement of momentum, say, after establishing a position correlation, will no longer yield any correlation in the momenta of the two particles. It is as if the position measurement disturbs the correlation between the momentum values, and conversely. Apart from this peculiarity that either correlation can be observed, but not both for the same pair of quantum particles, the position and momentum correlations for the quantum particles are exactly like the classical correlations between two billiard balls after a collision. Classical correlations can be explained by a common cause, or correlated ‘elements of reality.’ The EPR argument is that quantum mechanics is incomplete because these common causes or elements of reality are not included in the quantum state description.
Here is how Schrödinger put the puzzle in the first part of his two-part article (Schrödinger, 1935; p. 559):
Schrödinger coined the term ‘entanglement’ to describe this peculiar connection between quantum systems (Schrödinger, 1935; p. 555):
Most physicists attributed the puzzling features of entangled quantum states to Einstein’s inappropriate ‘detached observer’ view of physical theory and regarded Bohr’s reply to the EPR argument (Bohr, 1935) as vindicating the Copenhagen interpretation. This was unfortunate, because the study of entanglement was ignored for thirty years until John Bell’s reconsideration of the EPR argument (Bell, 1964). Bell looked at entanglement in simpler systems than the EPR example: matching correlations between two-valued dynamical quantities, such as polarization or spin, of two separated systems in an entangled state. What Bell showed was that the statistical correlations between the measurement outcomes of suitably chosen different quantities on the two systems are inconsistent with an inequality derivable from Einstein’s separability and locality assumptions — in effect from the assumption that the correlations have a common cause. This inequality is now known as Bell’s inequality, and various related inequalities can be derived as a necessary condition for classical or common cause correlations.
Bell’s investigation generated an ongoing debate on the foundations of quantum mechanics. One important feature of this debate was confirmation that entanglement can persist over long distances, thus falsifying Schrödinger’s supposition of the spontaneous decay of entanglement as two entangled particles separate. (Free space entanglement of photons has been confirmed in experiments between the Canary Islands of La Palma and Tenerife, a distance of 143 km. See Herbst et al 2014.) But it was not until the 1980s that physicists, computer scientists, and cryptologists began to regard the non-local correlations of entangled quantum states as a new kind of non-classical physical resource that could be exploited, rather than an embarrassment for quantum mechanics to be explained away. For a discussion of entanglement — what it is, why it is conceptually puzzling, and what you can do with it, including a simple proof of Bell’s theorem — see the graphic novel Totally Random: Why Nobody Understands Quantum Mechanics (A Serious Comic on Entanglement), Bub and Bub 2018. For further discussion of entanglement as a physical resource, including measuring entanglement, and the manipulation and purification of entanglement by local operations, see “The Joy of Entanglement” by Popescu and Rohrlich in Lo, Popescu, and Spiller 1998, Nielsen and Chuang 2000, or Bub 2016.
@Tony
@lutte
@Biiyo03
@volcelfatcel
@Preston
@StrangerDanger
@looksmaxxer234
@knajjd
@Thompsonz
Measurements of physical properties such as position, momentum, spin, and polarization performed on entangled particles can, in some cases, be found to be perfectly correlated. For example, if a pair of entangled particles is generated such that their total spin is known to be zero, and one particle is found to have clockwise spin on a first axis, then the spin of the other particle, measured on the same axis, is found to be counterclockwise. However, this behavior gives rise to seemingly paradoxical effects: any measurement of a particle's properties results in an irreversible wave function collapse of that particle and changes the original quantum state. With entangled particles, such measurements affect the entangled system as a whole.
Such phenomena were the subject of a 1935 paper by Albert Einstein, Boris Podolsky, and Nathan Rosen,[1] and several papers by Erwin Schrödinger shortly thereafter,[2][3] describing what came to be known as the EPR paradox. Einstein and others considered such behavior impossible, as it violated the local realism view of causality (Einstein referring to it as "spooky action at a distance")[4] and argued that the accepted formulation of quantum mechanics must therefore be incomplete.
Later, however, the counterintuitive predictions of quantum mechanics were verified[5][6][7] in tests where polarization or spin of entangled particles was measured at separate locations, statistically violating Bell's inequality. In earlier tests, it couldn't be ruled out that the result at one point could have been subtly transmitted to the remote point, affecting the outcome at the second location.[7] However, so-called "loophole-free" Bell tests have been performed where the locations were sufficiently separated that communications at the speed of light would have taken longer—in one case, 10,000 times longer—than the interval between the measurements.[6][5]
According to some interpretations of quantum mechanics, the effect of one measurement occurs instantly. Other interpretations which don't recognize wavefunction collapse dispute that there is any "effect" at all. However, all interpretations agree that entanglement produces correlation between the measurements and that the mutual information between the entangled particles can be exploited, but that any transmission of information at faster-than-light speeds is impossible.[8][9]
Quantum entanglement has been demonstrated experimentally with photons,[10][11] neutrinos,[12] electrons,[13][14] molecules as large as buckyballs,[15][16] and even small diamonds.[17][18] The utilization of entanglement in communication, computation and quantum radar is a very active area of research and development.

Spontaneous parametric down-conversion process can split photons into type II photon pairs with mutually perpendicular polarization.
History
The counterintuitive predictions of quantum mechanics about strongly correlated systems were first discussed by Albert Einstein in 1935, in a joint paper with Boris Podolsky and Nathan Rosen.[1] In this study, the three formulated the Einstein–Podolsky–Rosen paradox (EPR paradox), a thought experiment that attempted to show that "the quantum-mechanical description of physical reality given by wave functions is not complete."[1] However, the three scientists did not coin the word entanglement, nor did they generalize the special properties of the state they considered. Following the EPR paper, Erwin Schrödinger wrote a letter to Einstein in German in which he used the word Verschränkung (translated by himself as entanglement) "to describe the correlations between two particles that interact and then separate, as in the EPR experiment."[19]Schrödinger shortly thereafter published a seminal paper defining and discussing the notion of "entanglement." In the paper, he recognized the importance of the concept, and stated:[2] "I would not call [entanglement] one but rather the characteristic trait of quantum mechanics, the one that enforces its entire departure from classical lines of thought." Like Einstein, Schrödinger was dissatisfied with the concept of entanglement, because it seemed to violate the speed limit on the transmission of information implicit in the theory of relativity.[20] Einstein later famously derided entanglement as "spukhafte Fernwirkung"[21] or "spooky action at a distance."
The EPR paper generated significant interest among physicists, which inspired much discussion about the foundations of quantum mechanics (perhaps most famously Bohm's interpretation of quantum mechanics), but produced relatively little other published work. Despite the interest, the weak point in EPR's argument was not discovered until 1964, when John Stewart Bell proved that one of their key assumptions, the principle of locality, as applied to the kind of hidden variables interpretation hoped for by EPR, was mathematically inconsistent with the predictions of quantum theory.
Specifically, Bell demonstrated an upper limit, seen in Bell's inequality, regarding the strength of correlations that can be produced in any theory obeying local realism, and showed that quantum theory predicts violations of this limit for certain entangled systems.[22] His inequality is experimentally testable, and there have been numerous relevant experiments, starting with the pioneering work of Stuart Freedman and John Clauser in 1972[23] and Alain Aspect's experiments in 1982.[24] An early experimental breakthrough was due to Carl Kocher,[10][11] who already in 1967 presented an apparatus in which two photons successively emitted from a calcium atom were shown to be entangled – the first case of entangled visible light. The two photons passed diametrically positioned parallel polarizers with higher probability than classically predicted but with correlations in quantitative agreement with quantum mechanical calculations. He also showed that the correlation varied only upon (as cosine square of) the angle between the polarizer settings[11] and decreased exponentially with time lag between emitted photons.[25] Kocher’s apparatus, equipped with better polarizers, was used by Freedman and Clauser who could confirm the cosine square dependence and use it to demonstrate a violation of Bell’s inequality for a set of fixed angles.[23] All these experiments have shown agreement with quantum mechanics rather than the principle of local realism.
For decades, each had left open at least one loophole by which it was possible to question the validity of the results. However, in 2015 an experiment was performed that simultaneously closed both the detection and locality loopholes, and was heralded as "loophole-free"; this experiment ruled out a large class of local realism theories with certainty.[26] Alain Aspect notes that the "setting-independence loophole" – which he refers to as "far-fetched", yet, a "residual loophole" that "cannot be ignored" – has yet to be closed, and the free-will / superdeterminism loophole is unclosable; saying "no experiment, as ideal as it is, can be said to be totally loophole-free."[27]
Bell's work raised the possibility of using these super-strong correlations as a resource for communication. It led to the 1984 discovery of quantum key distribution protocols, most famously BB84 by Charles H. Bennett and Gilles Brassard[28] and E91 by Artur Ekert.[29] Although BB84 does not use entanglement, Ekert's protocol uses the violation of a Bell's inequality as a proof of security.

Article headline regarding the Einstein–Podolsky–Rosen paradox (EPR paradox) paper, in the May 4, 1935 issue of The New York Times.
Concept
Meaning of entanglement
An entangled system is defined to be one whose quantum state cannot be factored as a product of states of its local constituents; that is to say, they are not individual particles but are an inseparable whole. In entanglement, one constituent cannot be fully described without considering the other(s). The state of a composite system is always expressible as a sum, or superposition, of products of states of local constituents; it is entangled if this sum cannot be written as a single product term.Quantum systems can become entangled through various types of interactions. For some ways in which entanglement may be achieved for experimental purposes, see the section below on methods. Entanglement is broken when the entangled particles decohere through interaction with the environment; for example, when a measurement is made.[30]
As an example of entanglement: a subatomic particle decays into an entangled pair of other particles. The decay events obey the various conservation laws, and as a result, the measurement outcomes of one daughter particle must be highly correlated with the measurement outcomes of the other daughter particle (so that the total momenta, angular momenta, energy, and so forth remains roughly the same before and after this process). For instance, a spin-zero particle could decay into a pair of spin-½ particles. Since the total spin before and after this decay must be zero (conservation of angular momentum), whenever the first particle is measured to be spin up on some axis, the other, when measured on the same axis, is always found to be spin down. (This is called the spin anti-correlated case; and if the prior probabilities for measuring each spin are equal, the pair is said to be in the singlet state.)
The above result may or may not be perceived as surprising. A classical system would display the same property, and a hidden variable theory (see below) would certainly be required to do so, based on conservation of angular momentum in classical and quantum mechanics alike. The difference is that a classical system has definite values for all the observables all along, while the quantum system does not. In a sense to be discussed below, the quantum system considered here seems to acquire a probability distribution for the outcome of a measurement of the spin along any axis of the other particle upon measurement of the first particle. This probability distribution is in general different from what it would be without measurement of the first particle. This may certainly be perceived as surprising in the case of spatially separated entangled particles.
Paradox
The paradox is that a measurement made on either of the particles apparently collapses the state of the entire entangled system—and does so instantaneously, before any information about the measurement result could have been communicated to the other particle (assuming that information cannot travel faster than light) and hence assured the "proper" outcome of the measurement of the other part of the entangled pair. In the Copenhagen interpretation, the result of a spin measurement on one of the particles is a collapse into a state in which each particle has a definite spin (either up or down) along the axis of measurement. The outcome is taken to be random, with each possibility having a probability of 50%. However, if both spins are measured along the same axis, they are found to be anti-correlated. This means that the random outcome of the measurement made on one particle seems to have been transmitted to the other, so that it can make the "right choice" when it too is measured.[31]The distance and timing of the measurements can be chosen so as to make the interval between the two measurements spacelike, hence, any causal effect connecting the events would have to travel faster than light. According to the principles of special relativity, it is not possible for any information to travel between two such measuring events. It is not even possible to say which of the measurements came first. For two spacelike separated events x1 and x2 there are inertial frames in which x1 is first and others in which x2 is first. Therefore, the correlation between the two measurements cannot be explained as one measurement determining the other: different observers would disagree about the role of cause and effect.
(In fact similar paradoxes can arise even without entanglement: the position of a single particle is spread out over space, and two widely separated detectors attempting to detect the particle in two different places must instantaneously attain appropriate correlation, so that they do not both detect the particle.)
Hidden variables theory
A possible resolution to the paradox is to assume that quantum theory is incomplete, and the result of measurements depends on predetermined "hidden variables".[32] The state of the particles being measured contains some hidden variables, whose values effectively determine, right from the moment of separation, what the outcomes of the spin measurements are going to be. This would mean that each particle carries all the required information with it, and nothing needs to be transmitted from one particle to the other at the time of measurement. Einstein and others (see the previous section) originally believed this was the only way out of the paradox, and the accepted quantum mechanical description (with a random measurement outcome) must be incomplete.Violations of Bell's inequality
Local hidden variable theories fail, however, when measurements of the spin of entangled particles along different axes are considered. If a large number of pairs of such measurements are made (on a large number of pairs of entangled particles), then statistically, if the local realist or hidden variables view were correct, the results would always satisfy Bell's inequality. A number of experiments have shown in practice that Bell's inequality is not satisfied. However, prior to 2015, all of these had loophole problems that were considered the most important by the community of physicists.[33][34] When measurements of the entangled particles are made in moving relativistic reference frames, in which each measurement (in its own relativistic time frame) occurs before the other, the measurement results remain correlated.[35][36]The fundamental issue about measuring spin along different axes is that these measurements cannot have definite values at the same time―they are incompatible in the sense that these measurements' maximum simultaneous precision is constrained by the uncertainty principle. This is contrary to what is found in classical physics, where any number of properties can be measured simultaneously with arbitrary accuracy. It has been proven mathematically that compatible measurements cannot show Bell-inequality-violating correlations,[37] and thus entanglement is a fundamentally non-classical phenomenon.
Notable experimental results proving quantum entanglement
The first experiment that verified Einstein's spooky action at a distance or entanglement was successfully corroborated in a lab by Chien-Shiung Wu and a colleague named I. Shaknov in 1949, and was published on new year's day in 1950. The result specifically proved the quantum correlations of a pair of photons.[38] In experiments in 2012 and 2013, polarization correlation was created between photons that never coexisted in time.[39][40] The authors claimed that this result was achieved by entanglement swapping between two pairs of entangled photons after measuring the polarization of one photon of the early pair, and that it proves that quantum non-locality applies not only to space but also to time.In three independent experiments in 2013 it was shown that classically communicated separable quantum states can be used to carry entangled states.[41] The first loophole-free Bell test was held in TU Delft in 2015 confirming the violation of Bell inequality.[42]
In August 2014, Brazilian researcher Gabriela Barreto Lemos and team were able to "take pictures" of objects using photons that had not interacted with the subjects, but were entangled with photons that did interact with such objects. Lemos, from the University of Vienna, is confident that this new quantum imaging technique could find application where low light imaging is imperative, in fields like biological or medical imaging.[43]
From 2016 various companies like IBM, Microsoft etc. have successfully created quantum computers and allowed developers and tech enthusiasts to openly experiment with concepts of quantum mechanics including quantum entanglement.[44]
Mystery of time
There have been suggestions to look at the concept of time as an emergent phenomenon that is a side effect of quantum entanglement.[45][46] In other words, time is an entanglement phenomenon, which places all equal clock readings (of correctly prepared clocks, or of any objects usable as clocks) into the same history. This was first fully theorized by Don Page and William Wootters in 1983.[47] The Wheeler–DeWitt equation that combines general relativity and quantum mechanics – by leaving out time altogether – was introduced in the 1960s and it was taken up again in 1983, when Page and Wootters made a solution based on quantum entanglement. Page and Wootters argued that entanglement can be used to measure time.[48]Emergent gravity
Based on AdS/CFT correspondence, Mark Van Raamsdonk suggested that spacetime arises as an emergent phenomenon of the quantum degrees of freedom that are entangled and live in the boundary of the space-time.[49] Induced gravity can emerge from the entanglement first law.[50][51]Non-locality and entanglement
In the media and popular science, quantum non-locality is often portrayed as being equivalent to entanglement. While this is true for pure bipartite quantum states, in general entanglement is only necessary for non-local correlations, but there exist mixed entangled states that do not produce such correlations.[52] A well-known example is the Werner states that are entangled for certain values of {\displaystyle p_{sym}}, but can always be described using local hidden variables.[53] Moreover, it was shown that, for arbitrary numbers of parties, there exist states that are genuinely entangled but admit a local model.[54] The mentioned proofs about the existence of local models assume that there is only one copy of the quantum state available at a time. If the parties are allowed to perform local measurements on many copies of such states, then many apparently local states (e.g., the qubit Werner states) can no longer be described by a local model. This is, in particular, true for all distillable states. However, it remains an open question whether all entangled states become non-local given sufficiently many copies.[55]In short, entanglement of a state shared by two parties is necessary but not sufficient for that state to be non-local. It is important to recognize that entanglement is more commonly viewed as an algebraic concept, noted for being a prerequisite to non-locality as well as to quantum teleportation and to superdense coding, whereas non-locality is defined according to experimental statistics and is much more involved with the foundations and interpretations of quantum mechanics.[56]
Quantum mechanical framework
The following subsections are for those with a good working knowledge of the formal, mathematical description of quantum mechanics, including familiarity with the formalism and theoretical framework developed in the articles: bra–ket notation and mathematical formulation of quantum mechanics.Pure states
Consider two arbitrary quantum systems A and B, with respective Hilbert spaces HA and HB. The Hilbert space of the composite system is the tensor product{\displaystyle H_{A}\otimes H_{B}.}
If the first system is in state {\displaystyle \scriptstyle |\psi \rangle _{A}} and the second in state {\displaystyle \scriptstyle |\phi \rangle _{B}}, the state of the composite system is
{\displaystyle |\psi \rangle _{A}\otimes |\phi \rangle _{B}.}
States of the composite system that can be represented in this form are called separable states, or product states.
Not all states are separable states (and thus product states). Fix a basis {\displaystyle \scriptstyle \{|i\rangle _{A}\}} for HA and a basis {\displaystyle \scriptstyle \{|j\rangle _{B}\}} for HB. The most general state in HA ⊗ HB is of the form
{\displaystyle |\psi \rangle _{AB}=\sum _{i,j}c_{ij}|i\rangle _{A}\otimes |j\rangle _{B}}
This state is separable if there exist vectors {\displaystyle \scriptstyle [c_{i}^{A}],[c_{j}^{B}]} so that {\displaystyle \scriptstyle c_{ij}=c_{i}^{A}c_{j}^{B},}
For example, given two basis vectors {\displaystyle \scriptstyle \{|0\rangle _{A},|1\rangle _{A}\}} of HA and two basis vectors {\displaystyle \scriptstyle \{|0\rangle _{B},|1\rangle _{B}\}} of HB, the following is an entangled state:
{\displaystyle {\tfrac {1}{\sqrt {2}}}\left(|0\rangle _{A}\otimes |1\rangle _{B}-|1\rangle _{A}\otimes |0\rangle _{B}\right).}
If the composite system is in this state, it is impossible to attribute to either system A or system B a definite pure state. Another way to say this is that while the von Neumann entropy of the whole state is zero (as it is for any pure state), the entropy of the subsystems is greater than zero. In this sense, the systems are "entangled". This has specific empirical ramifications for interferometry.[57] The above example is one of four Bell states, which are (maximally) entangled pure states (pure states of the HA ⊗ HB space, but which cannot be separated into pure states of each HA and HB).
Now suppose Alice is an observer for system A, and Bob is an observer for system B. If in the entangled state given above Alice makes a measurement in the {\displaystyle \scriptstyle \{|0\rangle ,|1\rangle \}} eigenbasis of A, there are two possible outcomes, occurring with equal probability:[58]
- Alice measures 0, and the state of the system collapses to {\displaystyle \scriptstyle |0\rangle _{A}|1\rangle _{B}}.
- Alice measures 1, and the state of the system collapses to {\displaystyle \scriptstyle |1\rangle _{A}|0\rangle _{B}}.
The outcome of Alice's measurement is random. Alice cannot decide which state to collapse the composite system into, and therefore cannot transmit information to Bob by acting on her system. Causality is thus preserved, in this particular scheme. For the general argument, see no-communication theorem.
Ensembles
As mentioned above, a state of a quantum system is given by a unit vector in a Hilbert space. More generally, if one has less information about the system, then one calls it an 'ensemble' and describes it by a density matrix, which is a positive-semidefinite matrix, or a trace class when the state space is infinite-dimensional, and has trace 1. Again, by the spectral theorem, such a matrix takes the general form:{\displaystyle \rho =\sum _{i}w_{i}|\alpha _{i}\rangle \langle \alpha _{i}|,}
where the wi are positive-valued probabilities (they sum up to 1), the vectors αi are unit vectors, and in the infinite-dimensional case, we would take the closure of such states in the trace norm. We can interpret ρ as representing an ensemble where wi is the proportion of the ensemble whose states are {\displaystyle |\alpha _{i}\rangle }. When a mixed state has rank 1, it therefore describes a 'pure ensemble'. When there is less than total information about the state of a quantum system we need density matrices to represent the state.
Experimentally, a mixed ensemble might be realized as follows. Consider a "black box" apparatus that spits electrons towards an observer. The electrons' Hilbert spaces are identical. The apparatus might produce electrons that are all in the same state; in this case, the electrons received by the observer are then a pure ensemble. However, the apparatus could produce electrons in different states. For example, it could produce two populations of electrons: one with state {\displaystyle |\mathbf {z} +\rangle } with spins aligned in the positive z direction, and the other with state {\displaystyle |\mathbf {y} -\rangle }
Following the definition above, for a bipartite composite system, mixed states are just density matrices on HA ⊗ HB. That is, it has the general form
{\displaystyle \rho =\sum _{i}w_{i}\left[\sum _{j}{\bar {c}}_{ij}(|\alpha _{ij}\rangle \otimes |\beta _{ij}\rangle )\right]\left[\sum _{k}c_{ik}(\langle \alpha _{ik}|\otimes \langle \beta _{ik}|)\right]}
where the wi are positively valued probabilities, {\displaystyle \sum _{j}|c_{ij}|^{2}=1}, and the vectors are unit vectors. This is self-adjoint and positive and has trace 1.
Extending the definition of separability from the pure case, we say that a mixed state is separable if it can be written as[59]: 131–132
{\displaystyle \rho =\sum _{i}w_{i}\rho _{i}^{A}\otimes \rho _{i}^{B},}
where the wi are positively valued probabilities and the {\displaystyle \rho _{i}^{A}}'s and {\displaystyle \rho _{i}^{B}}'s are themselves mixed states (density operators) on the subsystems A and B respectively. In other words, a state is separable if it is a probability distribution over uncorrelated states, or product states. By writing the density matrices as sums of pure ensembles and expanding, we may assume without loss of generality that {\displaystyle \rho _{i}^{A}} and {\displaystyle \rho _{i}^{B}} are themselves pure ensembles. A state is then said to be entangled if it is not separable.
In general, finding out whether or not a mixed state is entangled is considered difficult. The general bipartite case has been shown to be NP-hard.[60] For the 2 × 2 and 2 × 3 cases, a necessary and sufficient criterion for separability is given by the famous Positive Partial Transpose (PPT) condition.[61]
Reduced density matrices
The idea of a reduced density matrix was introduced by Paul Dirac in 1930.[62] Consider as above systems A and B each with a Hilbert space HA, HB. Let the state of the composite system be{\displaystyle |\Psi \rangle \in H_{A}\otimes H_{B}.}
As indicated above, in general there is no way to associate a pure state to the component system A. However, it still is possible to associate a density matrix. Let
{\displaystyle \rho _{T}=|\Psi \rangle \;\langle \Psi |}
which is the projection operator onto this state. The state of A is the partial trace of ρT over the basis of system B:
{\displaystyle \rho _{A}\ {\stackrel {\mathrm {def} }{=}}\ \sum _{j}^{N_{B}}\left(I_{A}\otimes \langle j|_{B}\right)\left(|\Psi \rangle \langle \Psi |\right)\left(I_{A}\otimes |j\rangle _{B}\right)={\hbox{Tr}}_{B}\;\rho _{T}.}
The sum occurs over {\displaystyle N_{B}:=dim(H_{B})} and {\displaystyle I_{A}} the identity operator in {\displaystyle H_{A}}. ρA is sometimes called the reduced density matrix of ρ on subsystem A. Colloquially, we "trace out" system B to obtain the reduced density matrix on A.
For example, the reduced density matrix of A for the entangled state
{\displaystyle {\tfrac {1}{\sqrt {2}}}\left(|0\rangle _{A}\otimes |1\rangle _{B}-|1\rangle _{A}\otimes |0\rangle _{B}\right),}
discussed above is
{\displaystyle \rho _{A}={\tfrac {1}{2}}\left(|0\rangle _{A}\langle 0|_{A}+|1\rangle _{A}\langle 1|_{A}\right)}
This demonstrates that, as expected, the reduced density matrix for an entangled pure ensemble is a mixed ensemble. Also not surprisingly, the density matrix of A for the pure product state {\displaystyle |\psi \rangle _{A}\otimes |\phi \rangle _{B}} discussed above is
{\displaystyle \rho _{A}=|\psi \rangle _{A}\langle \psi |_{A}}.
In general, a bipartite pure state ρ is entangled if and only if its reduced states are mixed rather than pure.
Two applications that use them
Reduced density matrices were explicitly calculated in different spin chains with unique ground state. An example is the one-dimensional AKLT spin chain:[63] the ground state can be divided into a block and an environment. The reduced density matrix of the block is proportional to a projector to a degenerate ground state of another Hamiltonian.The reduced density matrix also was evaluated for XY spin chains, where it has full rank. It was proved that in the thermodynamic limit, the spectrum of the reduced density matrix of a large block of spins is an exact geometric sequence[64] in this case.
Entanglement as a resource
In quantum information theory, entangled states are considered a 'resource', i.e., something costly to produce and that allows to implement valuable transformations. The setting in which this perspective is most evident is that of "distant labs", i.e., two quantum systems labeled "A" and "B" on each of which arbitrary quantum operations can be performed, but which do not interact with each other quantum mechanically. The only interaction allowed is the exchange of classical information, which combined with the most general local quantum operations gives rise to the class of operations called LOCC (local operations and classical communication). These operations do not allow the production of entangled states between the systems A and B. But if A and B are provided with a supply of entangled states, then these, together with LOCC operations can enable a larger class of transformations. For example, an interaction between a qubit of A and a qubit of B can be realized by first teleporting A's qubit to B, then letting it interact with B's qubit (which is now a LOCC operation, since both qubits are in B's lab) and then teleporting the qubit back to A. Two maximally entangled states of two qubits are used up in this process. Thus entangled states are a resource that enables the realization of quantum interactions (or of quantum channels) in a setting where only LOCC are available, but they are consumed in the process. There are other applications where entanglement can be seen as a resource, e.g., private communication or distinguishing quantum states.[65]Classification of entanglement
Not all quantum states are equally valuable as a resource. To quantify this value, different entanglement measures (see below) can be used, that assign a numerical value to each quantum state. However, it is often interesting to settle for a coarser way to compare quantum states. This gives rise to different classification schemes. Most entanglement classes are defined based on whether states can be converted to other states using LOCC or a subclass of these operations. The smaller the set of allowed operations, the finer the classification. Important examples are:- If two states can be transformed into each other by a local unitary operation, they are said to be in the same LU class. This is the finest of the usually considered classes. Two states in the same LU class have the same value for entanglement measures and the same value as a resource in the distant-labs setting. There is an infinite number of different LU classes (even in the simplest case of two qubits in a pure state).[66][67]
- If two states can be transformed into each other by local operations including measurements with probability larger than 0, they are said to be in the same 'SLOCC class' ("stochastic LOCC"). Qualitatively, two states {\displaystyle \rho _{1}} and {\displaystyle \rho _{2}}in the same SLOCC class are equally powerful (since I can transform one into the other and then do whatever it allows me to do), but since the transformations {\displaystyle \rho _{1}\to \rho _{2}} and {\displaystyle \rho _{2}\to \rho _{1}} may succeed with different probability, they are no longer equally valuable. E.g., for two pure qubits there are only two SLOCC classes: the entangled states (which contains both the (maximally entangled) Bell states and weakly entangled states like {\displaystyle |00\rangle +0.01|11\rangle }) and the separable ones (i.e., product states like {\displaystyle |00\rangle }).[68][69]
- Instead of considering transformations of single copies of a state (like {\displaystyle \rho _{1}\to \rho _{2}}) one can define classes based on the possibility of multi-copy transformations. E.g., there are examples when {\displaystyle \rho _{1}\to \rho _{2}} is impossible by LOCC, but {\displaystyle \rho _{1}\otimes \rho _{1}\to \rho _{2}}is possible. A very important (and very coarse) classification is based on the property whether it is possible to transform an arbitrarily large number of copies of a state {\displaystyle \rho } into at least one pure entangled state. States that have this property are called distillable. These states are the most useful quantum states since, given enough of them, they can be transformed (with local operations) into any entangled state and hence allow for all possible uses. It came initially as a surprise that not all entangled states are distillable, those that are not are called 'bound entangled'.[70][65]
Entropy
In this section, the entropy of a mixed state is discussed as well as how it can be viewed as a measure of quantum entanglement.Definition

The plot of von Neumann entropy Vs Eigenvalue for a bipartite 2-level pure state. When the eigenvalue has value .5, von Neumann entropy is at a maximum, corresponding to maximum entanglement.
In classical information theory H, the Shannon entropy, is associated to a probability distribution,{\displaystyle p_{1},\cdots ,p_{n}}
{\displaystyle H(p_{1},\cdots ,p_{n})=-\sum _{i}p_{i}\log _{2}p_{i}.}
Since a mixed state ρ is a probability distribution over an ensemble, this leads naturally to the definition of the von Neumann entropy:
{\displaystyle S(\rho )=-{\hbox{Tr}}\left(\rho \log _{2}{\rho }\right).}
In general, one uses the Borel functional calculus to calculate a non-polynomial function such as log2(ρ). If the nonnegative operator ρ acts on a finite-dimensional Hilbert space and has eigenvalues {\displaystyle \lambda _{1},\cdots ,\lambda _{n}}, log2(ρ) turns out to be nothing more than the operator with the same eigenvectors, but the eigenvalues {\displaystyle \log _{2}(\lambda _{1}),\cdots ,\log _{2}(\lambda _{n})}. The Shannon entropy is then:
{\displaystyle S(\rho )=-{\hbox{Tr}}\left(\rho \log _{2}{\rho }\right)=-\sum _{i}\lambda _{i}\log _{2}\lambda _{i}}
Since an event of probability 0 should not contribute to the entropy, and given that
{\displaystyle \lim _{p\to 0}p\log p=0,}
the convention 0 log(0) = 0 is adopted. This extends to the infinite-dimensional case as well: if ρ has spectral resolution
{\displaystyle \rho =\int \lambda dP_{\lambda },}
assume the same convention when calculating
{\displaystyle \rho \log _{2}\rho =\int \lambda \log _{2}\lambda dP_{\lambda }.}
As in statistical mechanics, the more uncertainty (number of microstates) the system should possess, the larger the entropy. For example, the entropy of any pure state is zero, which is unsurprising since there is no uncertainty about a system in a pure state. The entropy of any of the two subsystems of the entangled state discussed above is log(2) (which can be shown to be the maximum entropy for 2 × 2 mixed states).
As a measure of entanglement
Entropy provides one tool that can be used to quantify entanglement, although other entanglement measures exist.[73] If the overall system is pure, the entropy of one subsystem can be used to measure its degree of entanglement with the other subsystems.For bipartite pure states, the von Neumann entropy of reduced states is the unique measure of entanglement in the sense that it is the only function on the family of states that satisfies certain axioms required of an entanglement measure[citation needed].
It is a classical result that the Shannon entropy achieves its maximum at, and only at, the uniform probability distribution {1/n,...,1/n}. Therefore, a bipartite pure state ρ ∈ HA ⊗ HB is said to be a maximally entangled state if the reduced state of each subsystem of ρ is the diagonal matrix
{\displaystyle {\begin{bmatrix}{\frac {1}{n}}&&\\&\ddots &\\&&{\frac {1}{n}}\end{bmatrix}}.}
For mixed states, the reduced von Neumann entropy is not the only reasonable entanglement measure.
As an aside, the information-theoretic definition is closely related to entropy in the sense of statistical mechanics[citation needed] (comparing the two definitions in the present context, it is customary to set the Boltzmann constant k = 1). For example, by properties of the Borel functional calculus, we see that for any unitary operator U,
{\displaystyle S(\rho )=S\left(U\rho U^{*}\right).}
Indeed, without this property, the von Neumann entropy would not be well-defined.
In particular, U could be the time evolution operator of the system, i.e.,
{\displaystyle U(t)=\exp \left({\frac {-iHt}{\hbar }}\right),}
where H is the Hamiltonian of the system. Here the entropy is unchanged.
The reversibility of a process is associated with the resulting entropy change, i.e., a process is reversible if, and only if, it leaves the entropy of the system invariant. Therefore, the march of the arrow of time towards thermodynamic equilibrium is simply the growing spread of quantum entanglement.[74] This provides a connection between quantum information theory and thermodynamics.
Rényi entropy also can be used as a measure of entanglement.
Entanglement measures
Entanglement measures quantify the amount of entanglement in a (often viewed as a bipartite) quantum state. As aforementioned, entanglement entropy is the standard measure of entanglement for pure states (but no longer a measure of entanglement for mixed states). For mixed states, there are some entanglement measures in the literature[73] and no single one is standard.- Entanglement cost
- Distillable entanglement
- Entanglement of formation
- Relative entropy of entanglement
- Squashed entanglement
- Logarithmic negativity
Quantum field theory
The Reeh-Schlieder theorem of quantum field theory is sometimes seen as an analogue of quantum entanglement.Applications
Entanglement has many applications in quantum information theory. With the aid of entanglement, otherwise impossible tasks may be achieved.Among the best-known applications of entanglement are superdense coding and quantum teleportation.[76]
Most researchers believe that entanglement is necessary to realize quantum computing (although this is disputed by some).[77]
Entanglement is used in some protocols of quantum cryptography.[78][79] This is because the "shared noise" of entanglement makes for an excellent one-time pad. Moreover, since measurement of either member of an entangled pair destroys the entanglement they share, entanglement-based quantum cryptography allows the sender and receiver to more easily detect the presence of an interceptor.[citation needed]
In interferometry, entanglement is necessary for surpassing the standard quantum limit and achieving the Heisenberg limit.[80]
Entangled states
There are several canonical entangled states that appear often in theory and experiments.For two qubits, the Bell states are
{\displaystyle |\Phi ^{\pm }\rangle ={\frac {1}{\sqrt {2}}}(|0\rangle _{A}\otimes |0\rangle _{B}\pm |1\rangle _{A}\otimes |1\rangle _{B})}
These four pure states are all maximally entangled (according to the entropy of entanglement) and form an orthonormal basis (linear algebra) of the Hilbert space of the two qubits. They play a fundamental role in Bell's theorem.
For M>2 qubits, the GHZ state is
{\displaystyle |\mathrm {GHZ} \rangle ={\frac {|0\rangle ^{\otimes M}+|1\rangle ^{\otimes M}}{\sqrt {2}}},}
which reduces to the Bell state {\displaystyle |\Phi ^{+}\rangle } for {\displaystyle M=2}. The traditional GHZ state was defined for {\displaystyle M=3}. GHZ states are occasionally extended to qudits, i.e., systems of d rather than 2 dimensions.
Also for M>2 qubits, there are spin squeezed states.[81] Spin squeezed states are a class of squeezed coherent states satisfying certain restrictions on the uncertainty of spin measurements, and are necessarily entangled.[82] Spin squeezed states are good candidates for enhancing precision measurements using quantum entanglement.[83]
For two bosonic modes, a NOON state is
{\displaystyle |\psi _{\text{NOON}}\rangle ={\frac {|N\rangle _{a}|0\rangle _{b}+|{0}\rangle _{a}|{N}\rangle _{b}}{\sqrt {2}}},\,}
This is like the Bell state {\displaystyle |\Psi ^{+}\rangle } except the basis kets 0 and 1 have been replaced with "the N photons are in one mode" and "the N photons are in the other mode".
Finally, there also exist twin Fock states for bosonic modes, which can be created by feeding a Fock state into two arms leading to a beam splitter. They are the sum of multiple of NOON states, and can used to achieve the Heisenberg limit.[84]
For the appropriately chosen measure of entanglement, Bell, GHZ, and NOON states are maximally entangled while spin squeezed and twin Fock states are only partially entangled. The partially entangled states are generally easier to prepare experimentally.
Methods of creating entanglement
Entanglement is usually created by direct interactions between subatomic particles. These interactions can take numerous forms. One of the most commonly used methods is spontaneous parametric down-conversion to generate a pair of photons entangled in polarisation.[65] Other methods include the use of a fiber coupler to confine and mix photons, photons emitted from decay cascade of the bi-exciton in a quantum dot,[85] the use of the Hong–Ou–Mandel effect, etc. In the earliest tests of Bell's theorem, the entangled particles were generated using atomic cascades.It is also possible to create entanglement between quantum systems that never directly interacted, through the use of entanglement swapping. Two independently prepared, identical particles may also be entangled if their wave functions merely spatially overlap, at least partially.[86]
Testing a system for entanglement
A density matrix ρ is called separable if it can be written as a convex sum of product states, namely{\displaystyle \displaystyle {\rho =\sum _{j}p_{j}\rho _{j}^{(A)}\otimes \rho _{j}^{(B)}}}
with {\displaystyle 1\geq p_{j}\geq 0} probabilities. By definition, a state is entangled if it is not separable.
For 2-Qubit and Qubit-Qutrit systems (2 × 2 and 2 × 3 respectively) the simple Peres–Horodecki criterion provides both a necessary and a sufficient criterion for separability, and thus—inadvertently—for detecting entanglement. However, for the general case, the criterion is merely a necessary one for separability, as the problem becomes NP-hard when generalized.[87][88] Other separability criteria include (but not limited to) the range criterion, reduction criterion, and those based on uncertainty relations.[89][90][91][92] See Ref.[93] for a review of separability criteria in discrete-variable systems and Ref.[94] for a review on techniques and challenges in experimental entanglement certification in discrete-variable systems.
A numerical approach to the problem is suggested by Jon Magne Leinaas, Jan Myrheim and Eirik Ovrum in their paper "Geometrical aspects of entanglement".[95] Leinaas et al. offer a numerical approach, iteratively refining an estimated separable state towards the target state to be tested, and checking if the target state can indeed be reached. An implementation of the algorithm (including a built-in Peres-Horodecki criterion testing) is "StateSeparator" web-app.
In continuous variable systems, the Peres-Horodecki criterion also applies. Specifically, Simon[96] formulated a particular version of the Peres-Horodecki criterion in terms of the second-order moments of canonical operators and showed that it is necessary and sufficient for {\displaystyle 1\oplus 1}-mode Gaussian states (see Ref.[97] for a seemingly different but essentially equivalent approach). It was later found[98] that Simon's condition is also necessary and sufficient for {\displaystyle 1\oplus n}-mode Gaussian states, but no longer sufficient for {\displaystyle 2\oplus 2}-mode Gaussian states. Simon's condition can be generalized by taking into account the higher order moments of canonical operators[99][100] or by using entropic measures.[101][102]
In 2016 China launched the world’s first quantum communications satellite.[103] The $100m Quantum Experiments at Space Scale (QUESS) mission was launched on Aug 16, 2016, from the Jiuquan Satellite Launch Center in northern China at 01:40 local time.
For the next two years, the craft – nicknamed "Micius" after the ancient Chinese philosopher – will demonstrate the feasibility of quantum communication between Earth and space, and test quantum entanglement over unprecedented distances.
In the June 16, 2017, issue of Science, Yin et al. report setting a new quantum entanglement distance record of 1,203 km, demonstrating the survival of a two-photon pair and a violation of a Bell inequality, reaching a CHSH valuation of 2.37 ± 0.09, under strict Einstein locality conditions, from the Micius satellite to bases in Lijian, Yunnan and Delingha, Quinhai, increasing the efficiency of transmission over prior fiberoptic experiments by an order of magnitude.[104][105]
Naturally entangled systems
The electron shells of multi-electron atoms always consist of entangled electrons. The correct ionization energy can be calculated only by consideration of electron entanglement.[106]Photosynthesis
It has been suggested that in the process of photosynthesis, entanglement is involved in the transfer of energy between light-harvesting complexes and photosynthetic reaction centers where kinetic energy in light is harvested in the form of chemical energy. Without such a process, the efficient conversion of light into chemical energy cannot be explained. Using femtosecond spectroscopy, the coherence of entanglement in the Fenna-Matthews-Olson complex was measured over hundreds of femtoseconds (a relatively long time in this regard) providing support to this theory.[107][108] However, critical follow-up studies question the interpretation of these results and assign the reported signatures of electronic quantum coherence to nuclear dynamics in the chromophores or to the experiments being performed at cryogenic rather than physiological temperatures.[109][110][111][112][113][114][115]
In 1935 and 1936, Schrödinger published a two-part article in the Proceedings of the Cambridge Philosophical Society in which he discussed and extended an argument by Einstein, Podolsky, and Rosen. The Einstein-Podolsky-Rosen (EPR) argument was, in many ways, the culmination of Einstein’s critique of the orthodox Copenhagen interpretation of quantum mechanics and was designed to show that the theory is incomplete. (See the entries on the Einstein-Podolsky-Rosen argument in quantum theory and the Copenhagen interpretation of quantum mechanics.) In classical mechanics the state of a system is essentially a list of the system’s properties — more precisely, it is the specification of a set of parameters from which the list of properties can be reconstructed: the positions and momenta of all the particles comprising the system (or similar parameters in the case of fields). The dynamics of the theory specifies how properties change in terms of a law of evolution for the state. In a letter to Max Born, Wolfgang Pauli characterized this mode of description of physical systems as a ‘detached observer’ idealization (see The Born-Einstein Letters, Born, 1992; p. 218). On the Copenhagen interpretation, such a description is not possible for quantum systems. Instead, the quantum state of a system should be understood as a catalogue of what an observer has done to the system and what has been observed, and the import of the state then lies in the probabilities that can be inferred (in terms of the theory) for the outcomes of possible future observations on the system. Einstein rejected this view and proposed a series of arguments to show that the quantum state is simply an incomplete characterization of a quantum system. The missing parameters are sometimes referred to as ‘hidden parameters’ or ‘hidden variables.’It should not be supposed that Einstein’s notion of a complete theory included the requirement that the theory should be deterministic. Rather, he required certain conditions of separability and locality for composite systems consisting of separated component systems: each component system separately should be characterized by its own properties (its own ‘being-thus,’ as Einstein put it — ‘So-sein’ in German), and it should be impossible to alter the properties of a distant system instantaneously (or the probabilities of these properties) by acting on a local system. In later analyses, notably in Bell’s argument for the nonlocality of quantum correlations, it became apparent that these conditions, suitably formulated as probability constraints, are equivalent to the requirement that statistical correlations between separated systems should be reducible to probability distributions over common causes (deterministic or stochastic) in the sense of Reichenbach. (See the entries on Bell’s theorem and Reichenbach’s common cause principle.)
In the original EPR article, two particles are prepared from a source in a certain ‘pure’ quantum state of the composite system (a state that cannot be expressed as a mixture or probability distribution of other pure quantum states, and cannot be reduced to a pure quantum state of each particle separately). After the particles move apart, there are ‘matching’ correlations between both the positions of the two particles and their momenta: a measurement of either position or momentum on a particular particle will allow the prediction, with certainty, of the outcome of a position measurement or momentum measurement, respectively, on the other particle. These measurements are mutually exclusive: either a position measurement can be performed, or a momentum measurement, but not both simultaneously. The subsequent measurement of momentum, say, after establishing a position correlation, will no longer yield any correlation in the momenta of the two particles. It is as if the position measurement disturbs the correlation between the momentum values, and conversely. Apart from this peculiarity that either correlation can be observed, but not both for the same pair of quantum particles, the position and momentum correlations for the quantum particles are exactly like the classical correlations between two billiard balls after a collision. Classical correlations can be explained by a common cause, or correlated ‘elements of reality.’ The EPR argument is that quantum mechanics is incomplete because these common causes or elements of reality are not included in the quantum state description.
Here is how Schrödinger put the puzzle in the first part of his two-part article (Schrödinger, 1935; p. 559):
What Schrödinger showed was that if two particles are prepared in an EPR quantum state, where there is a matching correlation between two ‘canonically conjugate’ dynamical quantities (quantities like position and momentum whose values suffice to specify all the properties of a classical system), then there are infinitely many dynamical quantities of the two particles for which there exist similar matching correlations: every function of the canonically conjugate pair of the first particle matches with the same function of the canonically conjugate pair of the second particle. So (Schrödinger, p. 559) system No. 1 ‘does not only know these two answers but a vast number of others, and that with no mnemotechnical help whatsoever, at least with none that we know of.’Yet since I can predict either x1x1 or p1p1 without interfering with the system No. 1 and since system No. 1, like a scholar in an examination, cannot possibly know which of the two questions I am going to ask first: it so seems that our scholar is prepared to give the right answer to the first question he is asked, anyhow. Therefore he must know both answers; which is an amazing knowledge; quite irrespective of the fact that after having given his first answer our scholar is invariably so disconcerted or tired out, that all the following answers are ‘wrong.’
Schrödinger coined the term ‘entanglement’ to describe this peculiar connection between quantum systems (Schrödinger, 1935; p. 555):
He added (Schrödinger, 1935; p. 555):When two systems, of which we know the states by their respective representatives, enter into temporary physical interaction due to known forces between them, and when after a time of mutual influence the systems separate again, then they can no longer be described in the same way as before, viz. by endowing each of them with a representative of its own. I would not call that one but rather the characteristic trait of quantum mechanics, the one that enforces its entire departure from classical lines of thought. By the interaction the two representatives [the quantum states] have become entangled.
In the second part of the paper, Schrödinger showed that an experimenter, by a suitable choice of operations carried out on one member of an entangled pair, possibly using additional ‘ancilla’ or helper particles, can ‘steer’ the second system into a chosen mixture of quantum states, with a probability distribution that depends on the entangled state. The second system cannot be steered into a particular quantum state at the whim of the experimenter, but for many copies of the entangled pair, the experimenter can constrain the quantum state of the second system to lie in a chosen set of quantum states, where these states are correlated with the possible outcomes of measurements carried out on the entangled paired systems, or the paired systems plus ancillas. He found this conclusion sufficiently unsettling to suggest that the entanglement between two separating systems would persist only for distances small enough that the time taken by light to travel from one system to the other could be neglected, compared with the characteristic time periods associated with other changes in the composite system. He speculated that for longer distances the two systems might in fact be in a correlated mixture of quantum states determined by the entangled state.Another way of expressing the peculiar situation is: the best possible knowledge of a whole does not necessarily include the best possible knowledge of all its parts,even though they may be entirely separate and therefore virtually capable of being ‘best possibly known,’ i.e., of possessing, each of them, a representative of its own. The lack of knowledge is by no means due to the interaction being insufficiently known — at least not in the way that it could possibly be known more completely — it is due to the interaction itself.
Attention has recently been called to the obvious but very disconcerting fact that even though we restrict the disentangling measurements to one system, the representative obtained for the other system is by no means independent of the particular choice of observations which we select for that purpose and which by the way are entirely arbitrary. It is rather discomforting that the theory should allow a system to be steered or piloted into one or the other type of state at the experimenter’s mercy in spite of his having no access to it.
Most physicists attributed the puzzling features of entangled quantum states to Einstein’s inappropriate ‘detached observer’ view of physical theory and regarded Bohr’s reply to the EPR argument (Bohr, 1935) as vindicating the Copenhagen interpretation. This was unfortunate, because the study of entanglement was ignored for thirty years until John Bell’s reconsideration of the EPR argument (Bell, 1964). Bell looked at entanglement in simpler systems than the EPR example: matching correlations between two-valued dynamical quantities, such as polarization or spin, of two separated systems in an entangled state. What Bell showed was that the statistical correlations between the measurement outcomes of suitably chosen different quantities on the two systems are inconsistent with an inequality derivable from Einstein’s separability and locality assumptions — in effect from the assumption that the correlations have a common cause. This inequality is now known as Bell’s inequality, and various related inequalities can be derived as a necessary condition for classical or common cause correlations.
Bell’s investigation generated an ongoing debate on the foundations of quantum mechanics. One important feature of this debate was confirmation that entanglement can persist over long distances, thus falsifying Schrödinger’s supposition of the spontaneous decay of entanglement as two entangled particles separate. (Free space entanglement of photons has been confirmed in experiments between the Canary Islands of La Palma and Tenerife, a distance of 143 km. See Herbst et al 2014.) But it was not until the 1980s that physicists, computer scientists, and cryptologists began to regard the non-local correlations of entangled quantum states as a new kind of non-classical physical resource that could be exploited, rather than an embarrassment for quantum mechanics to be explained away. For a discussion of entanglement — what it is, why it is conceptually puzzling, and what you can do with it, including a simple proof of Bell’s theorem — see the graphic novel Totally Random: Why Nobody Understands Quantum Mechanics (A Serious Comic on Entanglement), Bub and Bub 2018. For further discussion of entanglement as a physical resource, including measuring entanglement, and the manipulation and purification of entanglement by local operations, see “The Joy of Entanglement” by Popescu and Rohrlich in Lo, Popescu, and Spiller 1998, Nielsen and Chuang 2000, or Bub 2016.
TAGGING THE BROS:
@TsarTsar444@Tony
@lutte
@Biiyo03
@volcelfatcel
@Preston
@StrangerDanger
@looksmaxxer234
@knajjd
@Thompsonz






