wishIwasSalludon
leave this place behind
- Joined
- Nov 9, 2023
- Posts
- 17,031
- Reputation
- 22,624
Maxwell's equations, or Maxwell–Heaviside equations, are a set of coupled partial differential equations that, together with the Lorentz force law, form the foundation of classical electromagnetism, classical optics, electric and magnetic circuits. The equations provide a mathematical model for electric, optical, and radio technologies, such as power generation, electric motors, wirelesscommunication, lenses, radar, etc. They describe how electric and magnetic fields are generated by charges, currents, and changes of the fields.[note 1]The equations are named after the physicist and mathematician James Clerk Maxwell, who, in 1861 and 1862, published an early form of the equations that included the Lorentz force law. Maxwell first used the equations to propose that light is an electromagnetic phenomenon. The modern form of the equations in their most common formulation is credited to Oliver Heaviside.[1]
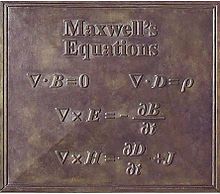Maxwell's equations on a plaque on his statue in Edinburgh
Maxwell's equations may be combined to demonstrate how fluctuations in electromagnetic fields (waves) propagate at a constant speed in vacuum, c (299792458 m/s[2]). Known as electromagnetic radiation, these waves occur at various wavelengths to produce a spectrum of radiation from radio waves to gamma rays.
In partial differential equation form and a coherent system of units, Maxwell's microscopic equations can be written as
With
the electric field,
the magnetic field,
the electric charge density and
the current density.
is the vacuum permittivity and
the vacuum permeability.
The equations have two major variants:
The publication of the equations marked the unification of a theory for previously separately described phenomena: magnetism, electricity, light, and associated radiation. Since the mid-20th century, it has been understood that Maxwell's equations do not give an exact description of electromagnetic phenomena, but are instead a classical limit of the more precise theory of quantum electrodynamics.
@cromagnon @ey88 @Gengar
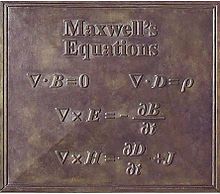Maxwell's equations on a plaque on his statue in EdinburghMaxwell's equations may be combined to demonstrate how fluctuations in electromagnetic fields (waves) propagate at a constant speed in vacuum, c (299792458 m/s[2]). Known as electromagnetic radiation, these waves occur at various wavelengths to produce a spectrum of radiation from radio waves to gamma rays.
In partial differential equation form and a coherent system of units, Maxwell's microscopic equations can be written as
The equations have two major variants:
- The microscopic equations have universal applicability but are unwieldy for common calculations. They relate the electric and magnetic fields to total charge and total current, including the complicated charges and currents in materials at the atomic scale.
- The macroscopic equations define two new auxiliary fields that describe the large-scale behaviour of matter without having to consider atomic-scale charges and quantum phenomena like spins. However, their use requires experimentally determined parameters for a phenomenological description of the electromagnetic response of materials.
The publication of the equations marked the unification of a theory for previously separately described phenomena: magnetism, electricity, light, and associated radiation. Since the mid-20th century, it has been understood that Maxwell's equations do not give an exact description of electromagnetic phenomena, but are instead a classical limit of the more precise theory of quantum electrodynamics.
@cromagnon @ey88 @Gengar
