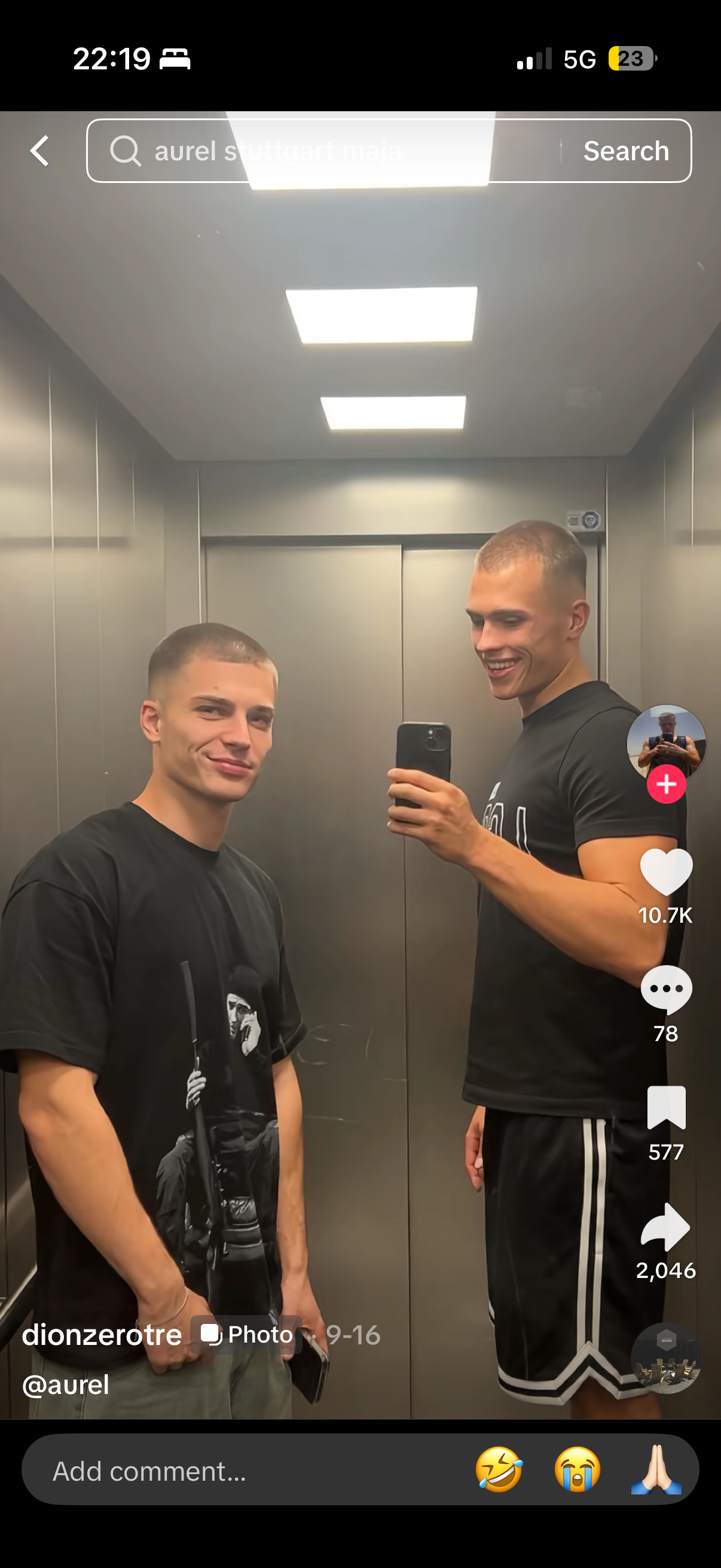
Gaygymmaxx
Top GGM (reformed brokie)
- Joined
- Mar 7, 2022
- Posts
- 63,740
- Reputation
- 108,176
@CantStopTheMog I just got faded after months off
Sheeit
Normal weed at moderate doses makes me introspective and look at my self like a foreign person, I immediately notice me and my brother are both across the room with headphones on and I'm like "holy shit this is not the way things were before, what a bizarre type of zoomer behavior"
But I'm just faded of d8 this is no good at all
Sheeit
Normal weed at moderate doses makes me introspective and look at my self like a foreign person, I immediately notice me and my brother are both across the room with headphones on and I'm like "holy shit this is not the way things were before, what a bizarre type of zoomer behavior"
But I'm just faded of d8 this is no good at all




 Now Truth and Liar must disagree between Q1 and Q2. Random is the only one who might by chance match or mismatch inconsistently.
Now Truth and Liar must disagree between Q1 and Q2. Random is the only one who might by chance match or mismatch inconsistently. The Setup
The Setup The Trick
The Trick Step-by-Step Strategy
Step-by-Step Strategy Result
Result