L
Lebgfinal
User
- Joined
- Jul 21, 2022
- Posts
- 19,191
- Reputation
- 28,423
Assume its 0.9 with infinite periods
Follow along with the video below to see how to install our site as a web app on your home screen.
Note: this_feature_currently_requires_accessing_site_using_safari
NoAssume its 0.9 with infinite periods
I think it is
test taken on robloxYou said your iq was tested at 128 with what test supposedly the same iq as @MoggerGaston
x = 0.9…Yes it is.
1/3=0.3333333.....
2/3=0.6666666.....
3/3=0.9999999.....
3/3=1
Therefore it's proven
I know the answer i just want to see what people will reply retardnigga trynna beat the low iq accusations
You would have to remove x on 9.9I think it is
x = 0.9…
10x = 9.9…
10x - x = 9.9… - 0.9…
9x = 9
x = 1
0.999… = 1
x is 0.9… ?You would have to remove x on 9.9
It would be this 10x-x= 9.9... -x
You said your iq was tested at 128 with what test supposedly the same iq as @MoggerGaston
brutal iq mogtest taken on roblox
Fuck I'm retarded give me a secx is 0.9… ?
Where he got his resultsYou said your iq was tested at 128 with what test supposedly the same iq as @MoggerGaston

I got my iq test in real life so yeah kysWhere he got his results
View attachment 3205389
9.9… has infinitely large decimals which mean is would need 0.001.. infinitely small decimalYes, in fact all numbers have in between infinite decimals, the distance from 1 to 2 implies that there are millions of numbers in between before reaching 2 or to reach 1, this principle is what is studied in calculus with respect to limits.
But indeed 0.99999 tends to 1 both on the left (-) and on the right (+), so it is indeed 1, (this is the calculation of lateral limits).
X=0.9~I think it is
x = 0.9…
10x = 9.9…
10x - x = 9.9… - 0.9…
9x = 9
x = 1
0.999… = 1
I know you don’t believe in Epigenetics but opinions on neuroplasticityI got my iq test in real life so yeah kys
that proof assumes 0.999 repeating is a real numberx = 0.9…
10x = 9.9…
10x - x = 9.9… - 0.9…
9x = 9
x = 1
0.999… = 1
Also proven with this
It assume 0.99999 has infinite decimals yeathat proof assumes 0.999 repeating is a real number
0,99999999 has infinite decimals thoX=0.9.
10x=9.9.
10x-x=9x=9.9.-0.9.= 8.9.
X=0.9.
@Lebgfinal
that proof assumes 0.999 repeating is a real number
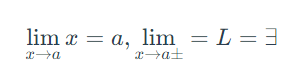
I took that into account let's take0,99999999 has infinite decimals tho
no, it assumes 0.999 repeating is a real number that exists. Also what u showed is not a proof, its just a series of true statements(based on that assumption). But it doesnt prove that 0.999=1It assume 0.99999 has infinite decimals yea
Use limits and understand his concept. Leibniz can answer your question.I took that into account let's take
0.9.+0.9.=1.9.
X+x= 2x
Which means that one of the 0.9. can't be bigger than the other so if you subtract 0.9. from 1.9. you'd get 0.9. the second 0.9. used 1 decimal to go from 0.9. to 1
This is hard to explain and I understand if you didn't understand this but in theory it can't become 1
Was my math right there?Use limits and understand his concept. Leibniz can answer your question.
most ppl arent talking about this when they're doing this so called 'proof'
yesAssume its 0.9 with infinite periods